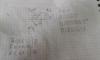Foro de preguntas y respuestas de Física

Antonio Silvio Palmitano
el 21/7/19

b)

Consideramos que el eje OX tiene sentido positivo hacia la derecha, que el eje OY tiene sentido positivo hacia arriba, y que el eje OZ tiene sentido positivo hacia la derecha, todo referido a la figura de tu enunciado, y observa que escribimos en negrita a las expresiones vectoriales.

Planteas la expresión vectorial del elemento de corriente, y queda:

IdL = < -IdL , 0 , 0 > (1).

Planteas la expresión vectorial de la posición del punto A con respecto a la posición del elemento de corriente que se muestra en tu figura, y queda:

r_A = < 0 , -R , 0 > (2), cuyo módulo tiene la expresión: │r_A│ = R (3).

Planteas la expresión vectorial de la posición del punto A con respecto a la posición del elemento de corriente que se muestra en tu figura, y queda:

r_P = < 0 , -R , 2R > (4), cuyo módulo tiene la expresión: │r_P│ = √(5)R (5).

Planteas la ecuación diferencial vectorial correspondiente a la Ley de Biot-Savart, y queda:

dB_P = ( μ₀/(4π) ) * (IdL x r_P)/r_P³,

sustituyes las expresiones vectoriales señaladas (1) (4), sustituyes la expresión escalar señalada (5), y queda:

dB_P = ( μ₀/(4π) ) * (< -IdL , 0 , 0 > x < 0 , -R , 2R >)/( √(5)R )³,

resuelves el producto vectorial, resuelves el cubo en el denominador escalary queda:

dB_P = ( μ₀/(4π) ) * < 0 , 2R*IdL , R*IdL >/ (5√(5)*R)³,

extraes los factores escalares (R*I) de la expresión vectorial, simplificas, asocias factores y divisores escalares, y queda:

dB_P = ( 5√(5)*μ₀*I/(4π) ) * < 0 , 2*dL , dL >/R² (6);

luego, observa que para todos los elementos de corriente que quieras considerar en la espira, tienes que su expresión vectorial es la expresión señalada (6), y observa además que sus componentes perpendiculares al eje OZ se compensan entre cada elemento de corriente y su elemento diametralmente opuesto, por lo que tienes que la componente significativa es la que corresponde al eje OZ, ya que las componentes en las direcciones perpendiculares a este eje coordenado se anulan, por lo que integras componente a componente para todos los puntos de la espira, y queda:

B_P = ₀∫^2πR ( 5√(5)*μ₀*I/(4π) ) * < 0 , 2*dL , dL >/R²,

extraes factores escalares, y queda:

B_P = ( 5√(5)*μ₀*I/(4π*R²) ) * ₀∫^2π*R < 0 , 0 , dL >,

resuelves la integral vectorial definida, y queda:

B_P = ( 5√(5)*μ₀*I/(4π*R²) ) * < 0 , 0 , 2π*R >,

extraes los factores escalares fuera de la expresión vectorial, y también fuera de la integral, y queda:

B_P = ( 5√(5)*μ₀*I/(4π*R²) )*2π*R * < 0 , 0 , 1 >,

simplificas expresiones escalares, y queda:

B_P = ( 5√(5)*μ₀*I/(2π*R) ) * < 0 , 0 , 1 >,

que es la expresión vectorial del campo magnético en el centro de la espira, cuyo módulo tiene la expresión:

│B_P│ =5√(5)* μ₀*I/(2π*R),

por lo que puedes concluir que la expresión señalada (18) no es la respuesta correcta.

Espero haberte ayudado.

jonathan vaccaro
el 8/7/19

hola buenas unicoos, quisiera me apoyen con una resolucion del sgte problema, hice la resolucion pero no tengo seguridad con las resp, adjunto eso tambien:

https://www.youtube.com/watch?v=3WWozOSZlj4

Raúl RC
el 8/7/19

Te recomiendo veas estos vídeos, porque el fundamento teórico que necesitas es el mismo:

https://www.youtube.com/watch?v=-xNKU5mdfL4

Nos cuentas ok? ;)

Antonio Silvio Palmitano
el 8/7/19

Vamos con una orientación.

Establece un sistema de referencia con instante inicial (t_i = 0) correspondiente a la partida de Kathy, con eje de posiciones OX con dirección y sentido positivo acordes al desplazamiento de los móviles, con origen de coordenadas en la línea de partida.

Luego, planteas las expresiones de las funciones de posición y de velocidad de Movimiento Rectilíneo Uniformemente Variado para ambos móviles (observa que sus instantes de partida son distintos, que resolvemos coeficientes y que cancelamos términos nulos), y queda:

para Kathy:

x = 2,45*t² (1a),

v = 4,90*t (1b);

para Stan (observa que parte un segundo antes que Kathy, por lo que se mueve un segundo más que ella):

x = 1,75*(t + 1)² (2a),

v = 3,50*t (2b).

a)

Planteas la condición de encuentro de los móviles, para ello igualas las expresiones señaladas (1a) y (2a), y queda la ecuación:

2,45*t² = 1,75*(t + 1)², desarrollas el segundo miembro, y queda:

2,45*t² = 1,75*t² + 3,50*t + 1,75, restas 1,75*t², restas 3,50*t y restas 1,75 en ambos miembros, reduces términos semejantes, y queda:

0,70*t² - 3,50*t - 1,75 = 0, divides por 0,70 en todos los términos de esta ecuación, y queda:

t² - 5*t - 2,5 = 0,

que es una ecuación polinómica cuadrática, cuyas soluciones son:

1º)

t = ( 5 - √(35) )/2 ≅ -0,458 s, que no tiene sentido para este problema;

2º)

t = ( 5 + √(35) )/2 ≅ 5,458 s,

b)

Aquí debes reemplazar el valor remarcado en la ecuación señalada (1a) y hacer el cálculo (te dejo la tarea).

c)

Aquí debes reemplazar el valor remarcado en las ecuaciones señaladas (1b) y (3b) y hacer los cálculos (te dejo la tarea).

Espero haberte ayudado.

Antonio Silvio Palmitano
el 11/7/19

Fe de errata.

En la ecuación señalada (2b) se me ha deslizado una omisión, la expresión correcta es:

v = 3,50*(t + 1).

Quiroga
el 7/7/19

Buenas alguien me puede decir como es la Ec y Ep en los nodos y vientres de una cuerda? Gracias.

Raúl RC
el 8/7/19

En los vientres la energía cinetica Ec=0 Ep=máxima

Nodos: Ec=max, Ep=0

Danilo Pin
el 7/7/19

Muy buenas tardes, tengo una duda, Ya eh intentado como 4 veces una y otra vez y no logro encontrar la respuesta. En la primera imagen está el Problema y en la segunda está las coordenadas rectangulares sacadas de cada uno de los vectores, dice que determine la relación pero no se como hacer eso si ya tengo las coordenadas. Ayuda por favor. Gracias.

Raúl RC
el 8/7/19

Prueba con esta pregunta en el foro de matemáticas, ya que es específica de alli, ok? ;)

Antonio Silvio Palmitano
el 11/7/19

Aquí puedes designar: v₁, v₂ y v₃ a los vectores que se encuentran en el primer cuadrante, en el segundo y en el tercero, respectivamente.

Luego, planteas las expresiones de dichos vectores, y queda:

v₁ = < 5P*cos(37°) , 5P*sen(37°) > ≅ < 3,993*P , 3,009*P >

v₂ = < -Q√(2)*cos(45°) , Q√(2)*sen(45°) > ≅ < -Q , Q >,

v₃ = < -4P√(3)*sen(30°) , -4P√(3)*cos(30°) > = < -2√(3)*P , -6*P >;

luego, planteas la expresión del vector resultante, y queda:

v = v₁ + v₂ + v₃,

sustituyes las expresiones de los vectores, resuelves la suma vectorial, y queda:

v ≅ < 3,993*P - Q - 2√(3)*P , 3,009*P + Q - 6*P >;

luego, como tienes en tu enunciado que el vector resultante tiene la dirección del eje OX, planteas que su segunda componente cuya expresión hemos remarcado es igual a cero, y queda la ecuación:

3,009*P + Q - 6*P ≅ 0,

aquí restas Q en ambos miembros, y queda:

3,009*P - 6*P ≅ -Q,

reduces términos semejantes en el primer miembro, y queda:

-2,991*P ≅ -Q,

sumas Q y sumas 2,991*P en ambos miembros, y queda:

Q ≅ 2,991*P,

y con las aproximaciones que hemos realizado, puedes concluir que la opción señalada:

Q = 3*P (D),

es la respuesta correcta.

Espero haberte ayudado.

David Avilés
el 6/7/19

Buenas noches :)

Chicos, tengo una gran duda...Me cuesta entender por qué la luz, una onda transversal y la perturbación en su campo electromagnético vibran en movimiento armónico simple? El movimiento armónico simple (mas) requiere de una fuerza restauradora para que el objeto oscilante se desplaza ida y vuelta respecto a su posición de equilibrio. No entiendo cómo se relaciona la luz con MAS. Espero no ocasionar molestia :(

Antonio Silvio Palmitano
el 7/7/19

Aquí vamos con una orientación, a muy grosso modo.

Recuerda que las fuerzas actúan sobre masas, sean partículas o sogas, por ejemplo, y algunas de ellas provocan el Movimiento Armónico Simple, si actúan, por ejemplo, sobre una partícula unida a un muelle, o la propagación de una onda transversal por una soga, en la que cada uno de sus puntos oscila con Movimiento Armónico Simple.

Con respecto a la luz, fue Maxwell quién formuló las leyes que permiten describir a la luz como ondas electromagnéticas, en la que un campo magnético y un campo eléctrico oscilan con direcciones perpendiculares entre sí, y también perpendiculares a la dirección de propagación de la onda luminosa, y propuso para ellos un modelo matemático muy similar al que conoces para el Movimiento Armónico simple.

Sería muy conveniente que busques textos sobre las Leyes de Maxwell, y elijas entre la infinidad que encontrarás, alguno acorde a tu nivel de estudios.

Espero haberte ayudado.