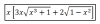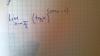Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

Keith Caballero Rodriguez
el 23/10/16

Me puede ayudar analizar la continuidad de f(x)=[3x]+sgn(x-4x^2), y en particular para x=2 , x=1/4, x=-5/4

••0 voto/s
•
Antonius Benedictus
el 23/10/16
¿Puedes poner foto del enunciado original?

•0 voto/s
•

Cancelar
Juanan PL
el 23/10/16

Discutir el siguiente sistema seg´un el valor de a, y hallar sus soluciones cuando sea posible.
2x − y = a
ax − 2y = 4
3x − y = 2

••0 voto/s
•
Antonius Benedictus
el 23/10/16
Te lo desarrollamos, Juana.

•1 voto/s
•

Cancelar
Matías
el 23/10/16

Como saco factor común "x" en el resultado H'(x)?

••0 voto/s
•
Antonius Benedictus
el 23/10/16
Así, Matías:

•0 voto/s
•

Cancelar
Gabriel
el 23/10/16

Buenas tardes. Tengo este limite para resolver por regla de lhopital
Aplico Ln para bajar el exponente y dejarlo de la forma 0.00.Despues paso el termino (senx-1)Dejandolo de la forma tgx/1/(senx-1) 00/00
El tema es que a partir de ahi, nose que hacer con el 1/(senx-1), porque si fuese 1/senx directamente cambio por cosecx pero al estar ese 1 restando, nose si me conviene derivar como fraccion ese termino..o si se hace algo mas.

••0 voto/s
•
Antonius Benedictus
el 23/10/16
Te lo explicamos, Gabriel:

•2 voto/s
•

Cancelar
andres
el 23/10/16

Buenas necesito ayuda con un ejercicio por favor: √512+√648-√128/81. Muchas gracias de antelación!

••0 voto/s
•
:)
el 23/10/16
primero separa teminos √512 + √648 - √128/81
luego hacer las raices √512 =22.6
√648 =25.4
primero realiza la division 128/81 =1.5 a ese resultado la raiz √1.5= 1.2
luego quedaria asi 22.6+25.4 -1.2 = 46.8 o mejor dicho 47

•0 voto/s
•
andres
el 23/10/16
Sí pero tiene que ser aplicando las potencias así me lo tachan

•0 voto/s
•
:)
el 23/10/16
para aplicar potencia hay que passarlo despues del igual y tu ahi no marc as esa opcion

•0 voto/s
•

Cancelar
Edgar Osuna
el 23/10/16

Mi duda es la siguiente, en primer lugar si el signo de más es igual si pongo el "°" para la función solicitada (antes del punto final). Y si es lo mismo decir "función a trozos" saludos desde México.
Dadas las funciones f(x)=|2x+1| y g(x)=|x-4| hallar la función por secciones para la función (f+g)(x) .

••0 voto/s
•
David
el 24/10/16
No es lo mismo f+g que fog.... Para hacer f+g, solo tienes que sumar la funciones...
Pero antes deberás dividir cada una de ellas en funciones a trozos...
f(x)=|2x+1| =
-2x-1 si x<=-1/2
2x+1 si x>=1/2...

g(x)=|x-4| =
-x+4=4-x si x<=4
x-4 si x>=4...

Al sumarlas, te quedarán tres trozos... (f+g)(x)
-2x-1+4-x=3-3x si x<=-1/2
2x+1+4-x=x+5 si 1/2<=x<=4
2x+1+x-4=3x-3 si x>=4...

•0 voto/s
•

Cancelar
Jordi García
el 23/10/16

Hola UNICOOS, tengo la siguiente duda:

¿Cuál es el criterio de divisibilidad de la tabla del 2 en base 9?
Por ejemplo, ¿cómo sabemos si el número 311 es divisible por 2 en base 9?

Gracias.

••0 voto/s
•
Antonio Silvio Palmitano
el 23/10/16
Una forma puede ser observando las cifras: como todas son impares, al multiplicarlas por potencias de 9 quedan resultados impares, y al sumarlos queda impar:
3*9^2 + 1*9 + 1 = 243 + 9 + 1 = 253 que es impar, por lo que no es múltiplo de 2.
En cambio, si tienes una cantidad par de cifras impares, y el resto de las cifras son pares, el número resultará múltiplo de 2 (indicamos expresión en base 9 entre paréntesis):
(325) = 3*9^2 + 2*9 + 5 = 243 + 18 + 5 = 266 que es impar, por lo que si es múltiplo de 2.
Por lo tanto, un criterio de divisibilidad por 2 para números expresados en base 9 puede ser:
Contar cuántas cifres impares tiene, y si es una cantidad par, el número será divisible por 2.
Espero haberte ayudado.

•0 voto/s
•

Cancelar
Daniel Pineda
el 23/10/16

Estudia la convergencia puntual y uniforme de la serie de funciones de termino general (1/n)*((x+1)/x)^n en el intervalo [−2, −1].

la convergencia puntual la tengo demostrada pero y la uniforme? no pueo utilizar el criterio mayorante de Weierstrass.

••0 voto/s
•
David
el 24/10/16
Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. Lo siento de corazón… Espero lo entiendas

•0 voto/s
•

Cancelar
cinthya
el 23/10/16

Hola, ¿podria alguien ayudarme con este problema de matrices?
¿Quien sera la matriz inversa de M ? Es el apartado b del ejercicio 2.
Gracias.

••0 voto/s
•
Monsif Ahlik
el 23/10/16
       el determinante es: a³
       la traspuesta de M es la misma que la matriz M
                                   a²   0        0
      adjunto de M= ( a²0       a²)
0       0       a²

         1/a^-1      0      0                                                                                    a      0      0
M^-1= ( 1/a^-1    0     1/a^-1 )    esto se puede poner de otra forma M^-1= ( a       0      a )
            0          0    1/a^-10       0      a
espero que no me haya equivocado, un saludo.


•1 voto/s
•
Antonius Benedictus
el 23/10/16
Va la respuesta, Cintia:

•1 voto/s
•

Cancelar
Ayleen
el 23/10/16

Buenos días! alguien me podría ayudar con el siguiente ejercicio? se los agradezco

••0 voto/s
•
David
el 24/10/16
Echales un vistazo y nos cuentas ¿ok?... Tienes uno casi idéntico... Propiedades de los determinantes

•0 voto/s
•

Cancelar