-
Daniel Morales
el 1/11/16 -
maite271098@gmail.com
el 1/11/16
Podrían explicarme el método de gram Schmidt?
-
Isabel Ester Arnal
el 1/11/16alguien podría ayudarme con esta ecuación log (base 5)/log (base 3)+log 3 z - 4 log (bajse 9)7
-
Ron Rc
el 1/11/16Podrian ayudarme con este ejercicio porfavor no entiendo como hacerlo llevo intentando todo el dia :( muchas gracias
Antonio Silvio Palmitano
el 1/11/16Observa que tienes dos puntos del plano buscado: A(3,1,-1) y B(0,0,-3), por lo que tienes que el vector que los une pertenece al plano:
u = AB = < 0-3 , 0-1 , -3+1 > = < -3 , -1 , -2 >, y este vector es perpendicular al vector normal del plano buscado (n).
Luego observa que el vector normal del plano perpendicular al plano buscado es: v = < 2 , -2 , 1 >, y por la condición de perpendicularidad entre planos, tenemos que el vector v es perpendicular al vector n.
Luego, como el vector n debe ser perpendicular a los vectores u y v a la vez, para obtener las componentes del vector n podemos plantear el producto vectorial:
n = u x v = < -3 , -1 , -2 > x < 2 , -2 , 1 > = < -5 , -1 , 8 >.
Luego, con el vector normal remarcado, y con el punto remarcado, podemos plantear la ecuación cartesiana implícita del plano buscado:
-5(x - 0) - 1(y - 0) + 8(z + 3) = 0, cancelamos términos nulos en los agrupamientos, distribuimos y queda:
-5x - y + 8z + 24 = 0, que es una ecuación del plano buscado.
Espero haberte ayudado.
-
Francisco Javier Cardama
el 1/11/16Buenas, tengo examen de matrices y determinantes mañana y me gustaría saber cual es la mejor forma de indicar el resultado de un ejercicio o si al menos las tres opciones que envio son correctas. El ejercicio es el típico de estudia el rango de la matriz según el parámetro "m". No estoy pidiendo ayuda con la resolución del ejercicio, si no la manera más correcta de indicar la solución, por lo cual no adjunto el enunciado.
Espero que me puedan ayudar, muchas gracias!
-
Samuel Alejandro
el 1/11/16 -
Celeste Martínez Martos
el 1/11/16He intentado hacer los ejercicios 13 y 14 pero... ¡no me salen! ayudaa😦😦
Francisco Javier Cardama
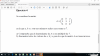
el 1/11/16En el ejercicio número 13 tienes que aplicar las propiedades de las potencias, separando 10^(x-2) en 10^x · 10^-2, haciendo lo mismo en el 10^(x-1), intentando que te queden únicamente 10^x. Cuando hayas hecho esto haces un cambio de variable y a 10^x lo llamas z, osea, z = 10^x y sustituyes. Hayas z como aparece en la imagen que te adjunto y deshaces el cambio, z = 10^x = 10^4
En el ejercicio número 14 tienes que despejar e^x como hago en la imagen y hacer el logaritmo neperiano en los dos lados. (el logaritmo neperiano de e^x = x porque el logaritmo de neperiano es un logaritmo con base el número "e")
-
Usuario eliminado
el 1/11/16 -
Lau
el 1/11/16Hola alguien me puede corregir este ejercico:
Y si podeis ayudarme con este otro ejercicio me quedo en la mitad:
-
Esperanza Macarena Diana Liroa
el 1/11/16Hola de nuevo;
tengo una duda con un problema de discontinuidad finita, me piden que de muestre que:
f(x)={1 x∈Q y -1 x∉Q
no es continua ¿me podéis echar una manita?, estoy un poco loca ya y no lo entiendo mucho.
Gracias :)
