-
Me podrian ayudar con esta demostración por inducción:
Si n>2 ∧ n∈Z+ entonces:
n ! > 2 n - 1


Antonio Silvio Palmitano
el 16/10/16Si la proposición es: n! > 2^(n-1), para n >2, n perteneciente al conjunto de los números naturales tenemos:
P(3): 3! > 2^(3-1), resolvemos y queda: 6 > 2^2, resolvemos a la derecha y queda. 6 > 4, por lo que tenemos que P(3) es Verdadera.
Hipótesis Inductiva, P(h): h! > 2^(h-1), para h > 2, h perteneciente al conjunto de los números naturales.
Tesis Inductiva, P(h+1): (h+1)! > 2^(h+1-1) = 2^h, h perteneciente al conjunto de los números naturales, h > 2.
Demostración (observa que h > 1, para todo h > 3, h perteneciente al conjunto de los números naturales (*)):
(h+1)! = (h+1)*h! > aplicamos la Hipótesis Inductiva > (h+1)*2^(h-1) > aplicamos la desigualdad señalada (*) > (1+1)*2^(h-1) = 2*2^(h-1) = 2^(1+h-1) = 2^h.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 16/10/16Puedes comenzar por plantear la sustitución (cambio de variable):
w = x^2, de donde tienes: dw = 2x*dx, y luego: dw/2 = x*dx, y observa también: x^4 = (x^2)^2 = w^2, luego sustituyes y la integral queda:
I = Integral V(1 - w^2)*(dw/2) = (1/2)*Integral V(1 - w^2)*dw
Luego, puedes plantear una nueva sustitución:
w = sent, de donde tienes: dw = cost*dt, y también tienes: V(1 - w^2) = V(1 - (sent)^2) = V((cost)^2) = cost, luego sustituyes y la integral queda:
I = (1/2)*Integral cost*cost*dt = (1/2)*Integral (cost)^2 * dt
Luego, puedes aplicar la sustitución trigonométrica: (cost)^2 = 1/2 + (1/2)*cos(2t), y queda para que termines la tarea.
Espero haberte ayudado.
-
hola unicoos, quisiera saber si me podrían ayudar con este problema, o como arranco para empezar a hacerlo?? gracias



Antonio Silvio Palmitano
el 15/10/16Indicamos theta como t y rho como r, luego la ecuación normal queda:
x*cost + y*sent - r = 0.
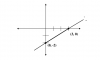
Luego, a partir de la gráfica tenemos que:
el punto de coordenadas (3,0) pertenece a la recta, por lo que reemplazamos sus coordenadas en la ecuación y queda:
3*cost + 0*sent - r = 0, que al resolver el segundo término de la izquierda queda: 3*cost - r = 0;
el punto de coordenadas (0,-2) pertenece a la recta, por lo que reemplazamos sus coordenadas en la ecuación y queda:
0*cost - 2*sent - r = 0, que al resolver el primer término de la izquierda queda: - 2*sent - r = 0.
Por lo tanto, nos queda el sistema de dos ecuaciones con dos incógnitas:
3*cost - r = 0, del que podemos despejar: 3*cost = r (*) (observa que cost es positivo, ya que r es positivo)
-2*sent - r = 0, del que podemos despejar: -2*sent = r (**), (observa que sent es negativo, ya que r es positivo)
luego igualamos y queda:
-2*sent = 3*cost, hacemos pasajes de factores como divisores y queda:
sent/cost = 3/(-2), sustituimos por identidad trigonométrica a la izquierda y resolvemos a la derecha y queda:
tant = -3/2,
luego, como tenemos que cost es positivo y sent es negativo, sabemos entonces que t pertenece al cuarto cuadrante, luego planteamos:
t = arctan(-3/2) = -56,31° + 360° = 303,69° (aproximadamente),
luego a partir de la ecuación señalada (*) reemplazas y tienes:
r = 3*cos(303,69°) = 1,66 (aproximadamente),
que puedes verificar reemplazando en la ecuación señalada (**).
Espero haberte ayudado.
-
Hoola gente, creo que todos los conjuntos de vectores menos el del apartado a) (ya que son solo dos vectores y faltaria un tercer vector tambien Li) son generadores de R3, ya que al hacer el determinante todos son distinto de 0, es decir que los vectores son Li. Pero despues como se si son base o no? Gracias!


Antonio Silvio Palmitano
el 15/10/16Vamos con cada ejercicio por separado:
a) Correcto, no es base porque necesitamos tres vectores linealmente independientes y solo tenemos dos.
b) Si es base, porque tienes tres vectores linealmente independientes.
c) No es base, ya que no tienes independencia lineal (observa que v3 = v1 - v2, por lo que el determinante debe darte nulo)
d) No es base ya que contiene cuatro vectores (sobraría uno), pero si es conjunto generador, ya que contiene a una base, cuyos elementos son v1, v2 y v4.
Espero haberte ayudado.
-
Me gustaría saber si me podrían dar alguna pista sobre cómo hacer este ejercicio con números factoriales.
Muchas gracias.


Antonio Silvio Palmitano
el 15/10/16En los ejercicios (a) y (d) se trata de desarrollar el factorial mayor hasta alcanzar el menor, para luego simplificar:
a) 12(k-2)! / k! = 12(k-2)! / ( k(k-1)(k-2)! ) = simplificamos = 12/( k(k-1) ), luego la ecuación queda:
12/( k(k-1) ) = 1, haces pasaje de divisor como factor y queda:
12 = k(k-1), distribuyes y queda:
12 = k^2 - k, haces pasajes de términos y queda:
- k^2 + k + 12 = 0, que es una ecuación polinómica cuadrática, aplicas la fórmula resolvente y obtienes las soluciones:
k1 = - 3, que no es un número natural
k2 = 4, que es una solución natural.
Queda para que intentes resolver el ejercicio (d).
Para los ejercicios (b) y (c), debemos desarrollar los números combinatorios. Para el ejercicio (b) tenemos:
k! / ( (k-2)! * ( k-(k-2) )! ) = K! / ( (k-2)! * 2! ) = desarrollamos el numerador = k*(k-1)*(k-2)! / ( (k-2)! * 2! ) = simplificamos = k*(k-1)/2! = k*(k-1)/2, luego queda:
k*(k-1)/2 = 10, hacemos pasaje de divisor como factor, distribuimos a la izquierda y queda:
k^2 - k = 20, hacemos pasaje de término y queda:
k^2 - k - 20 = 0, que es una ecuación polinómica cuadrática, aplicas la fórmula resolvente y tienes las soluciones:
k1 = -4, que no es un número natural,
k2 = 5, que si es un número natural.
Queda para que hagas el intento con el ejercicio (c).
Espero haberte ayudado.
-
Tenia que hacer esta ecuación de segundo grado de manera que lo igualé todo a 0 pero ahora no me queda la x, donde estuvo mi fallo?
-
Hola Unicoos estoy haciendo fracciones algebraicas y me hago un poco de lío, en lo que está rodeado en color rojo en el numerador, el -x² está multiplicando a (x+1)? O a (x+2) también? O tengo que quitar el paréntesis de (x+1) y dejarlo en x+1-x² ?
-


Antonio Silvio Palmitano
el 15/10/16Vas muy bien con tu planteo y, como debes establecer los valores de cuatro coeficientes, debes plantear la igualdad entre numeradores para cuatro valores distintos de x.
Ya lo has hecho para x1 = -1 y para x2 = -1/2, por lo que puedes elegir otros dos valores, por ejemplo: x3 = 0 y x4 = 1, y así obtendrás un sistema de cuatro ecuaciones con cuatro incógnitas que, al resolverlo, te conducirán a los valores de las constantes A, B, C y D que necesitas para resolver la integral.
Espero haberte ayudado.
-
Se me pide hallar todas las matrices cuadradas de orden 2 cuyo cuadrado sea nulo. No sé cómo continuar. Es el ejercicio de más abajo.



Antonio Silvio Palmitano
el 15/10/16Va una orientación: observa que en la segunda ecuación puedes factorizar, y queda:
c(a+d) = 0, que te conduce a dos opciones, que deberás desarrollar por separado:
a) c = 0, b) d = -a.
a) sustituimos en las demás ecuaciones, y el sistema queda:
a^2 = 0, de donde tienes a = 0
ab + bd = 0
d^2 = 0, de donde tienes d = 0
observa que la segunda ecuación verifica, para todo valor b, por lo tanto tenemos:
a = 0, b perteneciente a R, c = 0, d = 0.
b) Sustituimos en las demás ecuaciones y el sistema queda:
a^2 + bc = 0, observa que esta ecuación es igual a la tercera
ab + b(-a) = 0, observa que esta ecuación es una identidad verdadera
cb + a^2 = 0
veamos la tercera ecuación:
una solución es: a = 0, b = 0, c perteneciente a R, d = -0 = 0
otra solución es: a = 0, c = 0, b perteneciente a R, d = -0 = 0 (coincide con la solución de la opción a))
otra solución es: a perteneciente a R, b distinto de 0, c = -a^2 / b, d = -a.
Espero haberte ayudado.