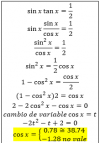-
Tomas
el 7/9/16Hola, ayuda porfavor
Antonio Silvio Palmitano
el 7/9/16Llamemos n al tamaño de la población (observa que n debe ser un número natural), por lo tanto planteamos:
C(n,2) = 45, luego desarrollamos el número combinatorio a la izquierda y queda:
n! / ( 2! * (n-2)! ) = 45, desarrollamos el numerador a la izquierda para poder simplificar y queda:
n*(n-1)*(n-2)! / ( 2! * (n-2)! ) = 45, simplificamos a la izquierda y queda:
n*(n-1) / 2! = 45, resolvemos el denominador a la izquierda y queda:
n*(n-1) / 2 = 45, hacemos pasaje de divisor como factor, resolvemos a la derecha y queda:
n*(n-1) = 90, distribuimos a la izquierda, hacemos pasaje de término y queda:
n^2 - n - 90 = 0, resolvemos la ecuación cuadrática con la fórmula de Baskara y obtenemos dos soluciones:
n1 = - 9, que no es solución para este problema porque -9 no pertenece al conjunto de los números naturales;
n2 = 10, si es la solución, ya que pertenece al conjunto de los números naturales, y podemos verificar que: C(10,2) = 45.
Por lo que concluimos que la opción D es la correcta.
Espero haberte ayudado.
-
Kevin Joshua JZ
el 7/9/16hola buen dia, me podrían ayudar para calcular el valor de theta en estos problemas, es que de verdad no entiendo como partir si no me dan ningún valor, hice un problema arriba que pense es parecido, pero ayuda porfa!
Kevin Joshua JZ
el 7/9/16
Desencadenado
el 7/9/16 -
Genesis Guzman
el 7/9/16Hola, tengo una duda de como graficar un funcion, donde primero tuve que calcular la pendiente de la tangente y luego graficar, pero nose si lo grafique bien :s
Genesis Guzman
el 7/9/16 -
Fernando
el 6/9/16Hola me ayudan con el ejercicio 27 c) no me sake como demostrarlo
Gracias
Antonio Silvio Palmitano
el 7/9/16A partir de la expresión general de un número complejo en forma binómica: z = x + yi , donde x e y son números reales (*), y de su conjugado. z' = x - yi, tenemos:
sen(iz') = sen( i(x - yi) ) = sen(ix + y) = sen(y + ix) = seny*cos(ix) + cosy*sen(ix) (observa que hemos aplicado la fórmula del seno de la suma de dos ángulos).
sen(iz) = sen( i(x + yi) ) = sen(ix - y) = sen(ix)*cosy - cos(ix)*seny (observa que hemos aplicado la fórmula del seno de la diferencia de dos ángulos).
Luego planteamos la igualdad entre las dos expresiones y tenemos:
seny*cos(ix) + cosy*sen(ix) = sen(ix)*cosy - cos(ix)*seny, cancelamos el segundo término de la izquierda y el primero de la derecha y queda:
seny*cos(ix) = - cos(ix)*seny, hacemos pasaje de término y reducimos términos a la izquierda y queda:
2*seny*cos(ix) = 0, hacemos pasaje de factor como divisor, resolvemos a la derecha y queda:
seny* cos(ix) = 0, observa que nos quedó un producto igualado a 0, por lo que tenemos dos opciones:
1)
seny = 0, de donde tenemos que: y = k*pi, con k perteneciente al conjunto de los números enteros;
2)
cos(ix) = 0, de donde tenemos que:
ix = (2k + 1)*pi/2, con k perteneciente al conjunto de los números enteros, luego multiplicamos por -i en ambos miembros, resolvemos a la izquierda y queda:
x = i(2k + 1)*pi/2, lo que es absurdo, porque plantea igualdad entre un número real a la izquierda, y un número imaginario a la derecha que no es nulo.
Por lo tanto, la igualdad se cumple para los valores que hemos encontrado en la primera opción:
y = k*pi, con k perteneciente al conjunto de los números enteros.
Espero haberte ayudado.
-
Natalia
el 6/9/16Hola, me gustaría que ayudaseis con esta ecuación: (x - 3)4 + √(x + 1) + (x - 82) = 0 Por más que lo intente siempre llego a un punto en el que me atasco.
-
The punk
el 6/9/16Hola amigos de unicoos me ayudan con esta demostración no la entiendo....
Antonio Silvio Palmitano
el 6/9/16Podemos expresar vectorialmente a las diagonales:
AC = AB + BC
BD = BC + CD
Luego, por propiedades de los rombos tenemos:
|AB| = |BC| = |CD| = L (L es la longitud del lado del rombo),
ángulo con vértice A = ángulo con vértice C = a
medida del ángulo con vértice B = medida del ángulo con vértice D = b
a + b = 180°.
Luego planteamos el producto escalar (lo indicamos con o) entre los vectores diagonales:
AC o BD = (AB + BC) o (BC + CD) = (recuerda que el producto escalar es distributivo con respecto a la suma)
= ABoBC + ABoCD + BCoBC + BCoCD =
(observa: AB = -BA, CD = BA, BC = -CB, por propiedades de los vectores equivalentes y de los vectores opuestos)
= -BAoBC + ABoBA + BCoBC - CBoCD =
(observa que resolvemos los productos escalares como producto de los módulos de los vectores por el coseno del ángulo comprendido entre ellos)
= - L^2 * cosb + L^2 * cosa + L^2 * cosb - L^2 * cosa = 0
(observa que los términos se cancelan dos a dos).
Luego, por propiedad de dos vectores perpendiculares (el producto escalar entre ellos es igual a cero), concluimos que AC es perpendicular a BD.
Puedes seguir todos estos pasos a partir del gráfico del enunciado.
Espero haberte ayudado.
-
Oscar Castro
el 6/9/16
He continuado resolviendo el ejercicio, los apartados e) y f) creo que los he resuelto correctamente ( a no ser que me haya equivocado en los cálculos) y los apartados g) y h) los he resulto como se ve en las imagenes pero no se si el planteamiento es correcto.¿Están los apartados g) y h) correctamente resueltos?
-
Jose Antonio Carrillo
el 6/9/16Hola tenia una duda sobre un ejercicio del teorema de Newton, en concreto que no se hacerlo con 2 funciones. Adjunto el ejercicio. Muchas gracias de antemano.
-
Gerardo
el 6/9/16Hola, estoy preparándome para un examen de Álgebra lineal Aplicada, mi duda es que en uno de los ejercicios me dice:
Muestre que para todo r perteneciente a todos los reales.X=-5+2r
Y=2+3r
z=3+2r
Es solución del sistema:
x + y + 2z - 5w =3
2x + 5y + z -9w=-3
x - 3y + 2z + 7w=-5
El sistema de arriba ya lo intente hacer por método de Gauss pero no me sale. Agradecería mucho que me pudieran ayudar.
César
el 6/9/16 -
Daniel Pineda
el 6/9/16Estoy estudiando teoria de grupos y hay una duda de que mata, ¿ Cuándo un grupo es cíclico ? se y entiendo perfectamente la definición de grupo ciclico lo que ocurre es que en algunos ejercicios me piden razonar sobre si el grupo es o no cíclico y es imposible razonar con la definición.He oído algo sobre si no es numerable... pero a lo que me refiero es: ¿ Hay algún teorema o alguna condición necesaria o suficiente para determinar si un grupo es ciclíco? gracias de antemano¡¡
César
el 6/9/16
