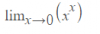ese sería la AV sólo te falta hacer el límite de x->∞ de la función para la AH ;-)

Observa que x tiende a cero por la derecha para que tenga sentido la expresión de la función. Puedes comenzar por plantear el logaritmo del límite que estamos calculando:

lnL = ln (Lím(x-->0+) (x^x) = Lím(x-->0+) ln(x^x) (observa que hemos aplicado propiedad del límite de una función continua) =

= (Lím(x-->0+) (x*lnx) (*) (observa que hemos aplicado la propiedad del logaritmo de una potencia).

Luego aplicamos la sustitución: w = 1/x

observa que w tiende a + infinito cuando x tiende a cero por la derecha, y que podemos despejar y queda: x = 1/w,

luego, si sustituimos en la expresión de la función queda:

x*lnx = (1/w)*ln(1/w) = (1/w)*(- lnw) = - lnw / w (observa que hemos aplicado la propiedad del logaritmo del inverso multiplicativo de w).

Luego sustituimos en la expresión señalada (*) y queda:

lnL = Lím(w-->+inf) (-lnw / w) = 0 (observa que por órdenes de magnitud, el logaritmo de w es mucho menor que w cuando w tiende a + infinito).

Luego observa que hemos llegado a la ecuación:

lnL = 0, componemos con la función inversa del logaritmo natural y queda:

e^(lnL) = e^0, resolvemos en ambos miembros y llegamos a:

L = 1.

Espero haberte ayudado.

porque elegiste el límite x->3?

de todas formas tu resultado esta bien Genesis

Es que en la pregunta del ejercicio me planteaban lo siguiente: f(x) = √x ; g(x) = x² + 4 .Determina que pasa con el Lim_{(x -->3)}  f(g(x))

a buena :) jejeje

Para justificar: observa que la función g es continua para x=3 y que g(3) = 13 , y que la función f también es continua para x=13 y que f(13) = V(13), por lo tanto puedes aplicar la propiedad del límite para una función continua:

Lím(x-->3) f( g(x) ) = (observa que f es continua) = f( Lím(x-->3) g(x) ) = f(13) = V(13).

Espero haberte ayudado.

Te sugiero los vídeos de OPTIMIZACION. En tu caso, puedes plantear que la diagonal mayor está dividida en dos trozos: x(el más pequeño) e y(el más grande). Por ello la diagonal mayor será x+y... Y la diagonal menor será 2x.... Por Pitagoras puedes deducir que x²+x²=a²..... 2x²=a²... √2. x = a... x=a/√2......
Y también que x²+y²=b².....y²=b²-x²..... y²=b²-a²/2..... y=√[b²-a²/2]

El área será A=D.d/2=(x+y). 2x / 2=(x+y).x= x²+x.y.. Espero esto te ayude a rrancar con el ejercicio

Se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. #nosvemosenclase Nos cuentas ¿ok?

Lo has resuelto correctamente.

Solo debes observar tu notación en la tercera línea: no es un binomio al cuadrado lo que tienes en el numerador, sino que es una diferencia de cuadrados, por lo tanto debes anotar:

( V(4x^2 + 9x - 5) )^2 - ( V(4x^2 + 4x +1) )^2.

Debes recordar la diferencia de cuadrados: (a+b)(a-b) = a^2 - b^2.

Y también el desarrollo de un binomio al cuadrado: (a-b)^2 = a^2 -2ab + b^2.

Espero haberte ayudado.

A.Vertical: haz el límite de x->4 si el límite te da ∞ ∃ AV en x=4

A. Horizontal: haz el límite de x->infinito si el límite te da un número existe AH en ese numero

espero lo que hagas mientras lo resuelvo ;-) 

No se puede aplicar la regla a una indeterminación ∞-∞

Solo si mediante alguna transformación algebraica, se consigue convertirla en otra 0/0  o ∞/∞ 

si, bueno, me he explicado mal, era a esa transformación a la que me refería

Solo tienes que derivar por independiente lo de arriba y lo de abajo del limite.

Va, Jordi: