-
No consigo solventar la indeterminación 0/0, ¿qué habría que hacer para solucionarlo? Me han dicho que el resultado es 1/2.
Gracias.

Antonio Silvio Palmitano
el 29/8/16Comencemos por tomar denominador común en la expresión de la función, lo haces y queda:
(e^x - 1 - x) / ( x*(e^x - 1) N/D (observa que N y D son expresiones de funciones derivables).
Luego, puedes aplicar la regla de L'Hôpital (derivar independientemente en el numerador y en el denominador), lo haces y queda:
N ' = e^x - 1 (observa que tiende a cero cuando x tiende a cero)
D ' = e^x - 1 + xe^x (observa que también tiende a cero cuando x tiende a cero)
por lo tanto, observando que seguimos tratando con expresiones derivables, volvemos a derivar y queda:
N '' = e^x (observa que tiende a uno cuando x tiende a cero)
D '' = 2e^x + xe^x (observa que tiende a dos cuando x tiende a cero).
Por lo tanto, a partir del límite planteado, hemos aplicado dos veces consecutivas la regla de L'Hôpital:
Lím(x-->0) N/D = Lím(x-->0) N '/D ' = Lím(x-->0) N ''/D'' = 1/2.
Otro camino para resolver el ejercicio, una vez tomado el denominador común en la expresión de la función, podría haber sido expresar a e^x por medio de su Polinomio de McLaurin (que se desarrolla alrededor de cero).
Espero haberte ayudado. -
-
1/3log en base 2 de X : -3
Por favor decirme como se haria y su resultado -


Antonio Silvio Palmitano
el 29/8/16Observa que podrías igualar las dos primeras ecuaciones, así eliminas el parámetro lambda, lo haces, y verás que los denominadores coinciden, por lo que los cancelas y llegas a y = x (*).
Luego sustituyes en la tercera ecuación y queda: x + x - 8 = 0, despejas y llegas a: x = 4.
Luego reemplazas e la ecuación señalada (*) y llegas a: y = 4.
Por último, reemplazas todo en la primera (o en la segunda) ecuación y obtienes:
lambda = 4/(2 + 4*4) = 1/9.
Espero haberte ayudado.

Antonio Silvio Palmitano
el 30/8/16Oberva que tienes tres ecuaciones con tres incógnitas (indicamos lambda como L):
y / (2 + xy) = L (*)
x / (2 + xy) = L
x + y - 8 = 0
Observa que, como L está despejado en las dos primeras ecuaciones, las podemos igualar, y mantener la tercera ecuación, por lo que nos queda el sistema de dos ecuaciones con dos incógnitas:
y / (2 + xy) = x / (2 + xy)
x + y - 8 = 0 (**)
Luego, en la primera ecuación, hacemos pasaje de divisor como factor y queda:
y = ( x / (2 + xy) ) * (2 + xy), observa que podemos simplificar la expresión del paréntesis, ya que multiplica y divide, lo hacemos y queda:
y = x (***)
luego, sustituimos en la ecuación señalada (**) y queda:
x + x - 8 = 0, reducimos términos semejantes, hacemos pasaje de término y queda:
2x = 8, hacemos pasaje de factor como divisor, resolvemos y queda:
x = 4,
luego reemplazamos en la ecuación señalada (***) y queda:
y = 4,
luego reemplazamos en la expresión señalada (*) y queda:
4 / (2 + 4*4) = L, resolvemos en el denominador y queda:
4/18 = L, simplificamos y llegamos a:
2/9 = L (aquí me toca corregir un error de tipeo en el anteúltimo renglón en mi entrega anterior, por favor disculpa).
Por lo tanto, la solución del sistema planteado es: x = 4, y = 4, L = 2/9:
Espero haberte ayudado. -


Antonio Silvio Palmitano
el 29/8/16Puedes plantear la sustitución (cambio de variable):
w = 1 + cos(2x), y el diferencial queda: dw = -2*sen(2x)*dx, luego despejas y queda: (-1/2)*dw = sen(2x)*dx.
Luego sustituyes y la integral queda:
I = (-1/2) * Integral (1/w)*dw = (-1/2)*ln|w| + C = (-1/2)*ln|1 + cos(2x)| + C.
Espero haberte ayudado.
-
Hola, tengo una duda con los logaritmos y ya he mirado los vídeo repetidas veces. Tengo un ejercicio que dice: 2log en base 2 de x=10. Creo que hay que utilizar la propiedad de nlogX=log^n, pero no se que hacer con el dos de la base. Ayuda por favor!!!



_Thumb.jpeg)

_Thumb.png)

_Thumb.png)
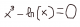
_Thumb.png)


_Thumb.jpg)



_Thumb.jpg)






_Thumb.jpg)


_Thumb.jpg)

