-
Buenas, no tengo ni idea de como hacer el siguiente ejercicio, a ver si pueden ayudarme por favor:
-Halla la ecuación de la recta tangente y la recta normal a la función f(x) en el punto de abcisa x=1.


Antonio Silvio Palmitano
el 17/8/16Con la información que has escrito, falta la expresión de la función.
Para plantear la ecuación de una recta necesitas uno de sus puntos (del que conoces solamente su abscisa x = 1, y te falta la ordenada y), y su pendiente.
La ordenada del punto de contacto se calcula evaluando la función, o sea: y = f(1), y el punto tiene coordenadas: (1 , f(1)).
La pendiente de la recta tangente se calcula evaluando la derivada de la función, o sea: mt = f ' (1)
Luego, puedes plantear la ecuación cartesiana de la recta tangente: y - f(1) = f ' (1) * (x - 1).
La recta normal es perpendicular a la recta tangente en el punto de contacto, por lo que su pendiente (recuerda la condición de perpendicularidad entre rectas) es: mn = -1/mt = -1/ f ' (1).
Luego, puedes plantear la ecuación cartesiana de la recta normal: y - f(1) = (-1/f ´(1)) * (x - 1).
Si conoces la expresión de la función f, puedes completar las ecuaciones.
Espero haberte ayudado. -
Hola, estoy intentando plantear este problema pero no estoy seguro cómo tengo que crear el siguiente sistema de ecuaciones, si sustituyendo x,y,z o alfa, beta, gamma
Gracias de antemano! -
HOLA GENTE, ALGUIEN ME PUEDE AYUDAR A RESOLVER ESTE SISTEMA POR EL METODO DE IGUALACION ????
b^2 + c^2 = 81
cb/2 = 10
GRACIAS DE ANTEMANO :) -
Hola unicoos!!!. No me sale el resultado y necesitaria despejar esta X. Lo he intentado varias veces y nada, por favor alguien que me ayude.
La solucion de la X aproximadamente es 0,188.
Un saludo y gracias!


Antonio Silvio Palmitano
el 17/8/16Observa que tienes una expresión fraccionaria:
el numerador es N = (x/2)*(x/2) = x^2 / 4;
el denominador es D = (0,4 - x) / 2;
luego, resolvemos el cociente:
N / D = ( x^2 / 4 ) / ((0,4 - x) / 2) = ( 2 * x^2 ) / ( 4 * (0,4 - x) = ( 2 * x^2 ) / (1,6 - 4x)
luego planteamos la ecuación:
N / D = 0,083
reemplazamos y queda:
( 2 * x^2 ) / (1,6 - 4x) = 0,083
hacemos pasaje de divisor como factor y queda:
2 * x^2 = 0,083*(1,6 - 4x)
distribuimos a la derecha y queda:
2 * x^2 = 0,1328 - 0,332x
hacemos pasajes de términos y queda:
2 * x^2 + 0,332x - 0,1328 = 0
dividimos en todos los términos por 2 y queda:
x^2 + 0,166x - 0,0664 = 0
observa que se trata de una ecuación polinómica cuadrática, aplicas la fórmula resolvente y llegas a sus dos soluciones:
x1 = 0,1877 (aproximadamente)
x2 = -0,3537 (aproximadamente)
Espero haberte ayudado. -


Antonio Silvio Palmitano
el 17/8/16Observa que tratas con una ecuación diferencial exacta, de la forma df = 0, cuya integral nos lleva a f(x,y) = C, donde fx = 2x + 1/y, fy = 1/y - x / y^2:
fx = 2x + 1/y, integramos con respecto a x y queda:
f = x^2 + x/y + A(y) (***)
luego derivamos con respecto a y y queda: fy = -x/y^2 + A'
luego comparamos:
-x/y^2 + A' = 1/y - x / y^2, cancelamos términos y queda:
A' = 1/y, luego integramos con respecto a y, y queda:
A(y) = ln|y| + K
por último, remplazamos en la expresión señalada (***) y obtenemos la solución general implícita (observa que agrupamos todas las constantes en una sola a la derecha):
f(x,y) = C, luego queda finalmente:
x^2 + x/y + ln|y| = C.
Espero haberte ayudado. -
Hola, tengo una duda sobre álgebra numérica, en el problema que adjunto en la imagen cómo podría comezar? no tengo lo que vale b y eso me impide poder empezarlo.
Muchas gracias!




_Thumb.png)



_Thumb.png)



_Thumb.png)




_Thumb.png)

_Thumb.png)


_Thumb.jpg)


_Thumb.jpg)
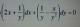
_Thumb.png)



_Thumb.jpg)
