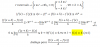Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

Guillem De La Calle Vicente
el 10/4/17

I es un intervalo, pudiendo ser de cualquier tipo.
Si f: I → ℛ es una función que cumple |f(x)-(y)| ≤ c · |x-y|^a, con a>1, c ∈ ℛ y x,y ∈ I arbitrarios, demuestre que f es constante.

••0 voto/s
•
Antonius Benedictus
el 10/4/17

•1 voto/s
•

Cancelar
Luciano Serra
el 10/4/17

Hola!. me piden determinar todos los valores de k tales que: el modulo de ΙΙAΙΙ = 1 si A = k.(2,2,1) resuelvo así: √((2K)²+(2K)²+(1K)²= 1 , reordeno tal que ----> √((4k)²+ k) =1 -----> (despejo la raíz)----> (4k²) + k² = 1 (acá se me abren dos posibilidades, o igualo a 0 y hago la fórmula de la raíz cuadrada o despejo k) (despejando queda así ---> 5k²= 1 ---> k²=1/5 k= √(1/2) = 1/25 . (cuando sustituyo a "k" por el resultado obtenido no me da la igualdad.. :S) si hago la fórmula de la cuadrática me queda (-2 (+ó-) √((1)²- 4.4.(-1)))/ 8 ----> (-1 (+ó-)√17)/ 8 = x₁=0,3903 x₂=-0,64038 . De por sí me quedan dos resultandos distintos si despejo k o si resuelvo con la formula. y cuando sustituyo a "k" por el valor obtenido tampoco me da la igualdad. Muchas gracias, Luciano!

••0 voto/s
•
Guillem De La Calle Vicente
el 10/4/17

•0 voto/s
•

Cancelar
Sergio R
el 10/4/17

Buenas tardes, ¿alguien podría darme una idea de cómo averiguo el mayor de los subconjuntos de R³ donde se cumple el teorema de la independecia del camino para un campo vectorial dado para integrales de línea?

••0 voto/s
•
Antonio Silvio Palmitano
el 10/4/17
Recuerda que deben cumplirse dos condiciones:
1°) Las componentes del campo vectorial deben ser continuas y tener derivadas parciales primeras continuas;
2°) El rotacional del campo vectorial debe ser nulo.
Por lo tanto, debes buscar el máximo conjunto D incluido en R³, en el que se cumplan las dos condiciones.
Espero haberte ayudado.

•0 voto/s
•
Sergio R
el 10/4/17
Si, lo de las condiciones lo tengo claro, es el hecho de dar con él lo que me pierde. No sé, pero no tengo idea de cómo empezarlo ahora mismo.
Y muchas gracias, porque si que ayuda, de verdad, se agradece

•0 voto/s
•

Cancelar
Francisco Bk Gtz
el 10/4/17

Las siguientes operaciones son correctas me piden simplificar al maximo pero ya no se como hacerlo mas.

••0 voto/s
•
Ángel
el 10/4/17
Intenta seguir factorizando los numeradores con Ruffini
http://www.vitutor.com/ab/p/a_12.html
http://www.unicoos.com/video/matematicas/4-eso/polinomios/regla-de-ruffini/division-de-polinomios-ruffini
Ahora nos cuentas.

•0 voto/s
•
Antonio Silvio Palmitano
el 10/4/17
Las expresiones están correctamente planteadas.
Luego, observa que no tienes factores comunes entre el numerador y el denominador, en ambas expresiones fraccionarias, por lo que ya son las mínimas expresiones posibles.
Luego, queda por aclarar que el dominio para ambas funciones es el conjunto: D = R - {0,5}.
Espero haberte ayudado.

•0 voto/s
•

Cancelar
Adrian Rojas
el 10/4/17

Hola, me dirían por favor que método uso para resolver esta integral? A simple vista parece Arctg pero como hago con la X^2 del numerador?
Desde ya gracias.

••0 voto/s
•
Guillem De La Calle Vicente
el 10/4/17

•1 voto/s
•
Antonio Silvio Palmitano
el 10/4/17
Vamos con una orientación.
Observa que la expresión de la función a integrar puede escribirse:
x²/(x² + 2) = ( (x² + 2) - 2 )/(x² + 2) = (x² + 2)/(x² + 2) - 2/(x² + 2) = 1 - 2/(x² + 2) = 1 - 2/(x² + (√(2))²).
Luego, tienes que para el primer término la integral es directa,
y para el segundo puedes aplicar la sustitución (cambio de vairable): x = √(2)*tanw.
Haz el intento de terminar la tarea, y si te es preciso no dudes en volver a consultar.
Espero haberte ayudado.

•1 voto/s
•

Cancelar
leo
el 10/4/17

Hola, me ayudan con esta demostracion de vectores ?

••0 voto/s
•
Antonio Silvio Palmitano
el 10/4/17
Vamos con un contraejemplo en R².
Puedes tomar los vectores: u = <1,0> y v = <0,1>.
Luego, observa que tienes: |u| = 1, |v| = 1, y |u+v| = |<1,1>| = √(1² + 1²) = √(2).
Luego, observa que tienes:
|u| + |v| = 1 + 1 = 2, ≠ √(2) = |u + v|.
Espero haberte ayudado.

•1 voto/s
•

Cancelar
Valeria
el 10/4/17

Buenas tardes, he realizado algunos ejercicios de derivadas, y quisiera que me los corrigieran. Gracias.
Perdòn por la imagen grr. :(

••0 voto/s
•
estudiantepuc
el 10/4/17
Hola! Si quieres saber las respuestas correctas, te recomiendo ir a página de wolfram alpha (al widget de derivadas) :).

Es muy simple y te da la respuesta de manera instantánea.
Saludos!

•0 voto/s
•
Ángel
el 10/4/17
No vas mal, las 4 primeras:

Están las 3 primeras bien y la segunda regular la simplificación.

•1 voto/s
•
Ángel
el 10/4/17

•1 voto/s
•
Ángel
el 10/4/17

•1 voto/s
•
Valeria
el 10/4/17
Para estudiante puc, gracias por la pag. solo que no me muestra el desarrollo.
Maths, gracias!!!

•0 voto/s
•

Cancelar
estudiantepuc
el 10/4/17

Hola! tengo una duda con un ejercicio de integrales (de las que van de "a" a "x"). Cuando me piden la derivada de la integra simplemente uso la integral que va desde "a" a "x" y luego uso regla de la cadena. el problema es que en este ejercicio me piden la derivada en un punto (que no es el del extremo superior de la integral original). ¿debería usar regla de la cadena y después evaluar la derivada en ese punto nuevo?
Yo sé obtener F'(x^2), pero no sé cómo sacar la derivada de un punto en específico luego de hacer todo el proceso para obtener la integral de la función original.
pd: me piden F'(pi/4)
Muchas gracias de antemano!!

••0 voto/s
•
Ángel
el 10/4/17
Para obtener la derivada en un punto específico tienes que poner en este caso pi/4 en cada lugar que haya una equis.

•1 voto/s
•
estudiantepuc
el 10/4/17
Eso sería lo lógico, o no? pero no me calza con el procedimiento que sale en la pauta. Y tú dices que tendría que reemplazar en F'(x) o en F'(X^2)?

Muchas gracias!

•0 voto/s
•
Ángel
el 10/4/17
La derivada de la integral de una función es la misma función, así que mucha complicación no tiene.
Si el ejercicio es ese y te piden que lo evalúes en un punto específico sustituyes pi/4 donde esté "x" y listo.
De todas maneras manda el enunciado original y lo aseguramos ;)

•1 voto/s
•

Cancelar
Sonsoles Retuerta Gil
el 10/4/17

En la pregunta 9 me indican que la respuesta es la b y yo creo que es la c, pq no especifican si, por ejemplo, las 3 monedas de plata pesan una onza cada una o entre las 3. ¿Cual sería el planteamiento correcto?

••0 voto/s
•
Ángel
el 10/4/17
Es la b)

•1 voto/s
•
Ángel
el 10/4/17
3x+2y=1220
2x+3y=1730
Resolviéndolo te da que x=550 euros la de oro e y=40 euros la de plata

Si tienes alguna duda pregunta.

•1 voto/s
•
Antonio Silvio Palmitano
el 10/4/17
Llamamos x al costo de una moneda de una onza de plata, y llamamos y al costo de media onza de oro.
Luego, tienes las ecuaciones:
3x + 2y = 1220
2x + 3y = 1730.
Luego, puedes resolver el sistema de ecuaciones, y su solución es: x = 40, y = 550.
Luego, el costo de dos monedas, con una de cada clase, es: 40 + 550 = 590 euros.
Espero haberte ayudado.

•1 voto/s
•

Cancelar