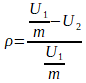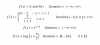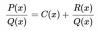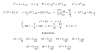-
- A ver tengo una pregunta, en una ecuación tal -> P(x)=x8 - 4x4 +5=0. Al convertirlo en x4 = t, y entender que t1 =4, entendemos que x4 =4 y por tanto x=+-4 √4. Mi pregunta es, si el indice de la raíz es cuatro, deberian ser cuatro las solucciones, siendo 2 negativos y 2 positivos ? y si el indice fuera 6 ? 3 positivos y 3 negativos las solucciones? y si fuera 5 el indice ? seria impar, cuales son las positivas y las negativas? 3 positivas y 2 negativas? o donde está esa regla no la encuentro. Muchas gracias


Jose Ramos
el 27/1/20Tus soluciones entran en el conjunto de los números complejos,, puesto que la raíz cuarta de 4 solo tiene dos soluciones en el conjunto de los reales. Si entramos en los complejos ya no podemos hablar de positivas y negativas porque en C no hay definida una relación de orden como en R. Por ejemplo 1 - i es un número complejo ni positivo ni negativo, (tiene la parte real positiva y la parte imaginaria negativa , pero considerado globalmente no tiene signo)
-


Antonio Silvio Palmitano
el 27/1/20Comienzas por multiplicar por U1/m en ambos miembros, y queda:
ρ*U1/m = U1/m - U2,
restas U1/m en ambos miembros, y queda:
ρ*U1/m - U1/m = -U2,
multiplicas por m en todos los términos, y queda:
ρ*U1 - U1 = -m*U2,
extraes factor común en el primer miembro, y queda:
(ρ - 1)*U1 = -m*U2,
divides por (ρ - 1) en ambos miembros (observa que esta expresión no debe tomar el valor cero), y queda:
U1 = -m*U2/(ρ - 1).
Espero haberte ayudado.
-
Hola buenas tardes, ¿me podrían ayudar con este problema? Dos capitaes que difieren en 2500 euros, se colocan al 4,5% de interés compuesto el mayor y al 6% el menor. Halla estos dos capitales sabiendo que en 20 años dan el mismo capital final. Gracias.
-
 alguien puede ayudarme con esta fracción simple de integrales? Lo unico q me acorde q cuando se tiene mayor exponente en el numerardo q en el denominador se hace la division desp de ahi n se si se multiplicaba el resto con el cociente ... alguien me ayuda ?porfis
alguien puede ayudarme con esta fracción simple de integrales? Lo unico q me acorde q cuando se tiene mayor exponente en el numerardo q en el denominador se hace la division desp de ahi n se si se multiplicaba el resto con el cociente ... alguien me ayuda ?porfis 

Francisco Javier Tinoco Tey
el 27/1/20

Antonio Silvio Palmitano
el 27/1/20Has efectuado la división del numerador del argumento de la integral entre su denominador (observa que también podrías haber aplicado la Regla de Ruffini).
Luego, recuerda que la fracción algebraica del argumento de la integral puede expresarse como una suma de dos términos:
el primero es el cociente que has obtenido (x2 - 4x + 16),
y el segundo es la división del resto que has obtenido entre el divisor (-64/[x+4]).
Luego, sustituyes la expresión del argumento, y la integral de tu enunciado queda:
I = ∫(x2 - 4x + 16 - 64/[x+4])*dx,
integras término a término, resuelves coeficientes, y queda:
I = (1/3)*x3 - 2*x2 + 16*x - 64*Ln(x+4) + C.
Espero haberte ayudado.
-


Breaking Vlad
el 27/1/20Hola! Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)


Antonio Silvio Palmitano
el 27/1/20Tienes la ecuación compleja:
i5*(zc)6 = 81*z2, resuelves el primer factor del primer miembro, y queda:
i*(zc)6 = 81*z2 (1).
Luego, expresas al número complejo genérico en forma exponencial, y queda:
z = |z|*ei*θ (2),
y la expresión del número complejo conjugado genérico queda (recuerda que el módulo del conjugado es igual al módulo del número complejo, y que su argumento es igual al opuesto del argumento del número complejo):
zc = |zc|*ei*(-θ) = |z|*e-i*θ (3);
luego, expresas a la unidad imaginaria en forma exponencial, y queda:
i = ei*π/2 (4).
Luego, sustituyes las expresiones señaladas (4) (3) (2) en la ecuación señalada (1), y queda:
ei*π/2*(|z|*e-i*θ)6 = 81*(|z|*ei*θ)2,
distribuyes las potencias y las resuelves en los segundos factores de ambos miembros, y queda:
ei*π/2*|z|6*e-i*6*θ = 81*|z|2*ei*2*θ,
divides por |z|2 en ambos miembros, y queda:
ei*π/2*|z|4*e-i*6*θ = 81*ei*2*θ,
multiplicas en ambos miembros, por e-i*2*θ, ordenas factores en el primer miembro, y queda:
|z|4*ei*π/2*e-i*6*θ*e-i*2*θ = 81,
aplicas la propiedad de una multiplicación de potencias con bases iguales en el primer miembro, resuelves el exponente, y queda:
|z|4*ei*(π/2-8*θ) = 81,
expresas al número real del segundo miembro en forma exponencial, y queda:
|z|4*ei*(π/2-8*θ) = 81*ei*2*k*π, con k ∈ Z (5).
Luego, por igualdad entre expresiones complejas en forma exponencial, igualas módulos e igualas argumentos en la ecuación señalada (5), y quedan las ecuaciones:
a)
|z|4 = 81, aquí extraes raíz cuarta real positiva en ambos miembros, y queda:
|z| = 3,
que es el valor del módulo de las soluciones de la ecuación de tu enunciado;
b)
i*(π/2 - 8*θ) = i*2*k*π, divides por i en ambos miembros, y queda:
π/2 - 8*θ = 2*k*π, multiplicas por 2 en todos los términos, y queda:
π - 16*θ = 4*k*π, restas π en ambos miembros, y queda:
-16*θ = -π + 4*k*π, multiplicas por -1 en todos los términos, y queda:
16*θ = π - 4*k*π, extraes factor común en el segundo miembro, luego divides por 16 en ambos miembros, y queda:
θ = (1 - 4*k)*π/16, con k ∈ Z (6),
que es la expresión general de los argumentos de las soluciones de la ecuación de tu enunciado;
luego, planteas la condición de argumento principal, y queda:
0 ≤ θ < 2π,
sustituyes la expresión señalada (6) en el miembro central de esta inecuación doble, y queda:
0 ≤ (1 - 4*k)*π/16 < 2π,
multiplicas por 16 y divides por π en los tres miembros de esta inecuación doble, y queda:
0 ≤ 1 - 4*k < 32,
restas 1 en los tres miembros de esta inecuación doble, y queda:
-1 ≤ -4*k < 31,
multiplicas por -1 en los tres miembros de esta inecuación doble (observa que cambian las desigualdades), y queda:
1 ≥ 4*k > -31,
divides por 4 en los tres miembros de esta inecuación doble (observa que no cambian las desigualdades), y queda:
1/4 ≥ k > -31/4,
expresas a los números racionales en forma decimal, y queda:
0,25 ≥ k > -7,75;
luego, como tienes en la expresión señalada (6) que el parámetro k debe tomar valores enteros, entonces tienes que sus valores posibles son:
k = -7, -6, -5, -4, -3, -2, -1 o 0.
Luego, planteas la expresión general de las soluciones de la ecuación de tu enunciado en forma exponencial, y queda:
zk = 3*ei*(1 - 4*k)*π/16, con k ∈ Z, con -7 ≤ k ≤ 0.
Espero haberte ayudado.
-
Hola únicos ¿por qué el límite cuando x tiende a dos por la izquierda del log(x cuadrado - 4) es menos infinito, e igualmente el límite cuando tiende a dos por la derecha es menos infinito? Gracias

gonzalezlbl
el 27/1/20El dominio de log(x2 - 4) = (-∞; -2) ∪ (2; +∞). Lo que nos dice que los números entre -2 y 2, incluyendo a ambos, NO existen en el dominio de la función,
por lo tanto el límite de esa función cuando x tiende a 2 por la izquierda, no existe.
Por la derecha de 2, la función tiende a -∞


Jose Ramos
el 27/1/20Cuando x tiende a 2 por la izquierda, el límite del log (x2- 4) no existe porque los valores de x2- 4 son negativos y el log no está definido para valores negativos. (El mismo argumento es válido cuando x tiende a -2 por la derecha)
Cuando x tiende a 2 por la derecha, el límite del log (x2- 4) el limite es -∞ porque los valores de x2- 4 son positivos y tan cercanos a 0 como se quiera y el log de un valor positivo, muy próximo a cero es un valor ENORME negativo, de ahí que el límite sea -∞. (Prueba en la calculadora el log de 0,00000001) (El mismo argumento es válido cuando x tiende a -2 por la izquierda)

gonzalezlbl
el 27/1/20Cuando x → 2+ (x tiende a 2 por la derecha), la expresión x2 - 4 tiende a cero por la derecha; es decir, se va haciendo más y más cercano a cero. Por ejemplo, vamos a hacer que x se acerque a 2 por la derecha de 2. (x toma valores mayores que 2, pero siempre acercándose a 2).
x = 3 entonces x2 - 4 = 5
x = 2.5 entonces x2 - 4 = 2.25
x = 2.3 entonces x2 - 4 = 1.29
x = 2.1 entonces x2 - 4 = 0.41
x = 2.01 entonces x2 - 4 = 0.0401
x = 2.001 entonces x2 - 4 = 0.004001
x = 2.0001 entonces x2 - 4 = 0.00040001
x → 2+ entonces x2 - 4 → 0+ (el + que se le coloca al cero indica que a medida que x tiende a 2 por encima de 2 (por su derecha), entonces x2 - 4 tiende a cero, pero con valores mayores que cero (números muy pequeños, pero positivos))
De la misma forma, en la medida que x2 - 4 → 0+ entonces log(x2 -4) → -∞ . Puedes verlo de forma gráfica o con otra tabla:
x = 3 entonces x2 - 4 = 5 y log(x2 - 4) ≈ 0.69897x = 2.5 entonces x2 - 4 = 2.25 y log(x2 - 4) ≈ 0.35218
x = 2.3 entonces x2 - 4 = 1.29 y log(x2 - 4) ≈ 0.11059
x = 2.1 entonces x2 - 4 = 0.41 y log(x2 - 4) ≈ - 0.38722
x = 2.01 entonces x2 - 4 = 0.0401 y log(x2 - 4) ≈ - 1.39686
x = 2.001 entonces x2 - 4 = 0.004001 y log(x2 - 4) ≈ - 2.39783
x = 2.0001 entonces x2 - 4 = 0.00040001 y log(x2 - 4) ≈ - 3.39793
En la medida que x2 - 4 se hace más pequeño (cercano a cero), su logaritmo se hace negativamente más grande.
Así
x → 2+ entonces x2 - 4 → 0+ y log(x2 - 4) → - ∞