Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

Marcos
el 1/12/16

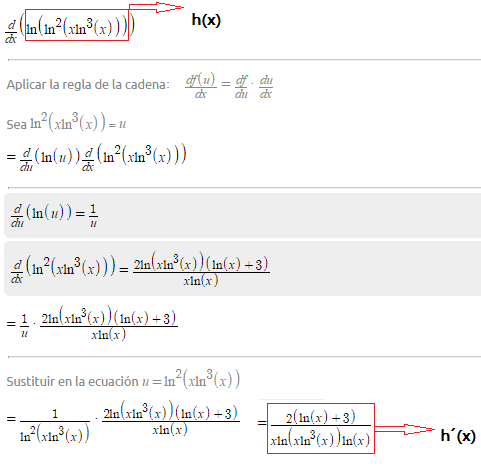
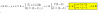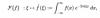Hola, tengo un problema con diagonalización de Matrices. El enunciado es el siguiente:
¿Qué debe verificar 𝛼 ∈ 𝑅 para que la matriz A sea diagonalizable?
He llegado hasta el calculo de autovectores de λ, y me queda que a = -a. No sé si es que hay que decir que no se puede diagonalizar, o que estoy haciendo algo mal. El determinante está bien hecho, lo he comprobado con una calculadora de matrices. Muchas gracias al buen samaritano que me ilumine el camino.

••0 voto/s
•
Antonius Benedictus
el 1/12/16
No se lee la matriz con claridad.

•0 voto/s
•
Marcos
el 1/12/16
La matriz es:

𝐴 = ( 1 𝛼 𝛼)
(−1 1 −1)
(1 0 2)

•0 voto/s
•
Antonius Benedictus
el 1/12/16

•0 voto/s
•

Cancelar
Pablo Arias Pampillón
el 1/12/16

Hola, buenas tardes, verán es que me estoy haciendo un lio con estos ejercicio: Sea {ū1,ū2,ū3} una base de R3 tal que |ū1| = 2, |ū2| = 3, |ū3| = 1. Teniendo en cuenta que ū1 * ū2 = 4, ū1 * ū3 = 3, ū2 * ū3 = 12, determina el valor de m Є IR para que los vectores siguientes sean ortogonales:

- ā = 11 ū1 + m ū2 + 3 ū3
- ē = 1 ū1 + 2 ū2 + 1 ū3

Llevo intentandolo hacer toda la mañana pero nada

••0 voto/s
•
Antonius Benedictus
el 1/12/16
Revisa las operaciones, Pablo. El proceso es correcto.

•1 voto/s
•
Pablo Arias Pampillón
el 1/12/16
Muchas gracias por ayudarme, pero no entiendo bien los pasos que sigues para calcular a * b, entiendo que es producto escalar pero no me pierdo cuando haces el producto de a y b (a * b)

•0 voto/s
•
Antonius Benedictus
el 1/12/16
Aplico las propiedades operativas del producto escalar:
Distributiva respecto de la suma. Homogénea (con el producto de un número por un vector). Conmutativa.

•1 voto/s
•
Pablo Arias Pampillón
el 1/12/16
Si, una parte la entiendo pero no entiendo lo que esta subrayado, no sé ahi en que parte estás multiplicando y sumando

•0 voto/s
•
Pablo Arias Pampillón
el 1/12/16
ahhh, ya lo acabo de entender, buff por fin jaja, ahora ya sé de donde venian aquellas sumas, gracias!

•0 voto/s
•

Cancelar
benson
el 1/12/16

Obtén las ecuaciones paramétricas de la recta r, que pasa por P(3, -2) y es perpendicular a la recta 2x-y+4=0

••0 voto/s
•
Antonius Benedictus
el 1/12/16

•0 voto/s
•

Cancelar
Jesús Martín Delgado
el 1/12/16

Sobre números complejos
cómo se hace x^2 = -2

••0 voto/s
•
Ángel
el 1/12/16

•0 voto/s
•

Cancelar
Xenia
el 1/12/16

Hola! No sé cómo resolver esta identidad trigonométrica, me podríais ayudar?
cos 2a = -2sen (a+45°) cos (a+45°)

••0 voto/s
•
Antonio Silvio Palmitano
el 1/12/16
Recuerda la identidad trgonométrica: sen(2x) = 2senxcosx, la aplicamos en el segundo miembro y queda:
cos(2a) = - sen( 2(a+45°) ), distribuimos en el argumento del seno y queda:
cos(2a) = - sen(2a+90°), luego aplicamos la identidad del seno de la suma de dos ángulos (sen(x+y) = senxcosy+cosxseny) y queda:
cos(2a) = - ( sen(2a)cos(90°) + cos(2a)sen(90°) ), resolvemos factores y queda:
cos(2a) = - ( sen(2a)*0 + cos(2a)*1 ), cancelamos el término nulo en el segundo miembro y queda:
cos(2a) = - cos(2a), hacemos pasaje de factor, reducimos términos semejantes y queda:
2cos(2a) = 0, dividimos por 2 en ambos miembros y queda:
cos(2a) = 0, componemos con la función inversa del coseno y quedan dos opciones:
a) 2a = 90° + 360°*k, con k ∈ Z, dividimos en todos los términos por 2 y queda:
a = 45° + 180°*k, con k ∈ Z;
b) 2a = 270° + 360°*k, con k ∈ Z, dividimos en todos los términos por 2 y queda:
a = 135° + 180°*k, con k ∈ Z.
Espero haberte ayudado.

•1 voto/s
•

Cancelar
Mario García García
el 1/12/16

Buenas! tengo una duda en como hacer el siguiente problema de optimización, más bien al hacer la derivada:
Sea un triangulo rectangulo de lados x y z cuyo perimetro es 3, se pide que el Area sea maxima.
x+y+z=3 Perimetro
A=1/2*x+y
z=√x^2+y^2
sustituyo en el el perimetro esa z y más tarde lo sustituyo en mi funcion, que es el area... pero tengo dos incognitas y no puedo derivar. Derivadas parciales aún no he dado...¿Alguien me puede ayudar?

••0 voto/s
•
Antonio Silvio Palmitano
el 1/12/16
Llamemos x e y a las longitudes de los catetos del triángulo rectángulo, y llamemos z a la longitud de su hipotenusa, luego tenemos (observa que x, y, z toman valores estrictamente mayores que cero):
z = √(x²+y²) (1),
luego sustituimos en la ecuación del perímetro (que es igual a 3) y queda:
x + y + √(x²+y²) = 3, hacemos pasajes de términos y queda:
√(x²+y²) = 3 - x - y, hacemos pasaje de raíz como potencia y queda:
x²+ y² = (3 - x - y)², desarrollamos el segundo miembro y queda:
x²+ y² = 9 + x²+ y² - 6x - 6y + 2xy, hacemos pasajes de términos, cancelamos términos semejantes y queda:
6y - 2xy = 9 - 6x, extraemos factor común en ambos miembros y queda:
2y(3 - x) = 3(3 - 2x), hacemos pasajes de factores como divisores y queda:
y = (3/2)(3 - 2x)/(3 - x) (2).
Luego pasamos a la expresión del área del triángulo rectángulo:
A = (1/2)xy, sustituimos según la ecuación señalada (2) y queda:
A = (1/2)x(3/2)(3 - 2x)/(3 - x), resolvemos factores numéricos y distribuimos el factor x en el numerador y queda:
A(x) = (3/4)(3x - 2x²)/(3 - x).
Luego puedes derivar, igualar a cero y continuar la tarea.
Espero haberte ayudado.

•1 voto/s
•

Cancelar
Gabriel Andrés Dehner
el 1/12/16

Buenas, cómo se lee la siguiente expresión? Desde ya muchas gracias. Saludos desde Argentina!

••0 voto/s
•
Ángel
el 1/12/16
Si el elemento f del conjunto F verifica epsilon, entonces el unitario de f verificará que es igual a la integral del área comprendida entre infinito e infinito de f(x) por e elevado a -2 pi, "i", "epsilon", "equis"

•2 voto/s
•

Cancelar
Eva
el 1/12/16

Hola me podrían ayudar con este ejercicio?
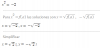
Una función f(x) continua en el intervalo [a,b] cumple que f(a)= -1 y f(b) = 3. ¿Puede asegurarse que la función toma solo valores comprendidos entre -1 y 3 en el intervalo [a,b]
Gracias :)

••0 voto/s
•
Ángel
el 1/12/16
No, además de f(a) y f(b) habría que estudiar las raíces de la primera derivada (f´(x)=0) y los puntos de no derivabilidad para saber cuales son los extremos absolutos, esto es, qué valores toma f(x)

•1 voto/s
•

Cancelar
DueFreitas
el 1/12/16

Profe nose como trabajar con esta.

••0 voto/s
•
Ángel
el 1/12/16

•1 voto/s
•

Cancelar
Nuria Azores
el 1/12/16

No se como resolverlo. A mi parecer no se puede resolver no? Gracias!

••0 voto/s
•
Antonio Silvio Palmitano
el 1/12/16
Llamemos x a la longitud de la base del triángulo, α a la medida del ángulo interior izquierdo y β a la medida del ángulo interior derecho, ubicados sobre la base.
Luego, aplicamos el Teorema del coseno:
x² = 5² + 8² - 2*5*8*cos(110°), resolvemos términos:
x² ≅ 25 + 64 + 27,36, resolvemos el segundo miembro:
x² ≅ 116,36, hacemos pasaje de potencia como raíz y queda:
x ≅ √(116,36), resolvemos y queda:
x ≅ 10,79 cm.
Luego, aplicamos el Teorema del seno:
sen(110°)/x = senα/8, hacemos pasaje de divisor como factor y queda:
8*sen(110°)/10,79 ≅ senα, resolvemos el primer miembro:
0,70 ≅ senα, componemos con la función inversa del seno y queda:
44,16° ≅ α.
Luego, aplicamos el Teorema del seno:
sen(110°) / x = senβ/5, hacemos pasaje de divisor como factor y queda:
5*sen(110°)/10,79 ≅ senβ, resolvemos el primer miembro:
0,44 ≅ senβ, componemos con la función inversa del seno y queda:
25,81° ≅ β.
Espero haberte ayudado.

•0 voto/s
•
M gales
el 1/12/16
Lo sabes hacer, solo te has comido él coseno en la fórmula por lo que veo.

•0 voto/s
•

Cancelar