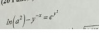-
threza
el 30/11/16
Hola, como puedo resolver este sistema de ecuaciones diferenciales
dx/dt=-ay+f(t)
dy/dt=-bx
Con valores iniciales; x(0)=0 , y(0)=51000
El resultado es este
Pero no se ni por donde empezar, agradecería algo de Orientacion con esta ecuacion diferenciial
saludos
David
el 30/11/16Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
Adrian Alex
el 30/11/16Buenas tengo este problema de aplicacion de derivadas. El ejercicio pide la ecuacion de la recta tangente a f(x)= X3 + 2X2 - 4X + 5 ,en los puntos en los cuales es paralela a la recta 2y+8x-5. Primero "transforme" la recta a y = -8x+5 / 2 , luego saque su derivada para obtener la pendiente que me dio -4, luego iguale la funcion a ese -4 quedandome , x(3x+4) = 0, y obtuve dos puntos x, x = 0 y x = -4/3. El problema que tengo es con el -4/3 ya que tratar de sacar su recta tangente da numeros muy complicados como 311/27 y siento que me he perdido. Eso es todo. Muchas gracias de antemano
-
Celeste
el 30/11/16Hola!! Tengo una duda de índole matemática (trigonométrica mas que nada) en un problema de física, espero estar en el foro correcto :D
El problema dice: Una masa de 0,5 kg está sujeta al extremo de un resorte horizontal. Para mantener el resorte estirado 10 cm se requiere aplicarle una fuerza de 2000 N. Cuando se comienza a describir el movimiento, el cuerpo se encuentra a 1,5 cm a la derecha de la posición de equilibrio con una velocidad de 0,40 m/s hacia la derecha. Determine constante elástica, período, Amplitud y fase inicial del movimiento.
Hasta el momento de calcular el periodo no tengo problemas, pero cuando obtengo el angulo de fase y la amplitud encuentro que tengo dos (o más) formas de realizar los despejes de las ecuaciones y no obtengo el mismo resultado!!
si utilizo x(t)=A cos (ωt+φ) como solución general obtengo φ=-0,042π y A=0,06 m
si utilizo x(t)=A sen (ωt+φ) como solución general obtengo φ=0,457π y A= 0,015 m (que creo que tiene más sentido), pero aún así no entiendo por qué debo usar tal o cual solución general (siendo que ambas cumplen con ser de solución de ecuación diferencial gral)
David
el 30/11/16Evidentemente no tiene nada que ver con matemáticas...
Te sugiero dejes tu duda en el foro de FÍSICA, pero antes, por favor, revisa los vídeos de MOVIMIENTO ARMONICO SIMPLE... Movimiento Armónico Simple
A partir de ahí, se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-) -
andres
el 30/11/16
Antonio Silvio Palmitano
el 30/11/16Observa que las expresiones de los trozos corresponden a funciones continuas, por lo que queda solamente estudiar los puntos de corte.
a) Para x = -1:
1) f(-1) = evaluamos en el segundo trozo = (-1)2 - 1 = 1 - 1 = 0;
2) límites laterales:
Lím(x->-1-) f(x) = Lím(x->-1-) (x+a) = -1 + a,
Lím(x->-1+) f(x) = Lím(x->-1+) (x2 - 1) = 0,
igualamos y queda: - 1 + a = 0, de donde despejamos: a = 1;
3) la función es continua en x = -1, si a = 1.
b) Para x = 1:
1) f(1) = evaluamos en el tercer trozo = ln(b);
2) límites laterales:
Lím(x->1-) f(x) = Lím(x->1-) (x2 - 1) = 0,
Lím(x->1+) f(x) = Lím(x->1+) ln(b) = ln(b),
igualamos y queda: ln(b) = 0, componemos con la función inversa del logaritmo natural y queda: b = e0= 1;
3) la función es continua en x = 1, si b = 1.
Espero haberte ayudado.
-
andres
el 30/11/16
Antonio Silvio Palmitano
el 30/11/16Vamos con los ejercicios, el primero por partes como te sugieren en el enunciado, y el segundo por sustitución.
a) Planteamos: u = 2x - 1, de donde tenemos: du = 2dx, luego: dv = 3xdx, de donde tenemos: v = 3x/ln3, luego aplicamos el método y queda:
I = uv - ∫ vdu = (2x - 1)3x/ln3 - (1/ln3) ∫ 3xdx = (2x - 1)3x/ln3 - (1/ln3)23x + C.
b) Planteamos la sustitución: w = x3 + 6x + 1, de donde tenemos: dw = (3x2 + 6)dx = 3(x2 + 2)dx, de donde despejamos: dw/3 = (x2 + 2)dx, luego sustituimos y queda:
I = (1/3) ∫ (1/w)dw = (1/3) lnw + C = (1/3) ln(x3 + 6x + 1) + C.
Espero haberte ayudado.
-
andres
el 30/11/16 -
DueFreitas
el 29/11/16 -
JöïïtHä Ëlïï?äbth
el 29/11/16buenas tardes ayuda..!! como encuentro la matriz inversa por el método de gauss dada la matriz
1 2 2
1 2 1
2 1 2
pofavor ayuda..!!
Antonio Silvio Palmitano
el 29/11/16Partimos de la matriz doble (a la izquierda la matriz A y a la derecha la matriz identidad de orden 3):
1 2 2 1 0 0
1 2 1 0 1 0
2 1 2 0 0 1
A la fila 2 le restamos la fila 1, y a la fila 3 le restamos el doble de la fila 1:
1 2 2 1 0 0
0 0 -1 -1 1 0
0 -3 -2 -2 0 1
Permutamos la fila 2 con la fila 3:
1 2 2 1 0 0
0 -3 -2 -2 0 1
0 0 -1 -1 1 0
Multiplicamos a la fila 2 por -1/3:
1 2 2 1 0 0
0 1 2/3 2/3 0 -1/3
0 0 -1 -1 1 0
A la fila 1 le restamos el doble de la fila 2:
1 0 2/3 -1/3 0 2/3
0 1 2/3 2/3 0 -1/3
0 0 -1 -1 1 0
A la fila 1 le sumamos la fila 3 multiplicada por 2/3, y a la fila 2 le sumamos la fila 3 multiplicada por 2/3:
1 0 0 -1 2/3 2/3
0 1 0 0 2/3 -1/3
0 0 -1 -1 1 0
Multiplicamos a la fila 3 por -1:
1 0 0 -1 2/3 2/3
0 1 0 0 2/3 -1/3
0 0 1 1 -1 0
Observa que a la izquierda tenemos la matriz identidad, y a la derecha la matriz inversa de la matriz A.
Recuerda que si la matriz A es invertible, tenemos que las mismas operaciones elementales que nos llevan desde la matriz A hasta la matriz identidad, son las que nos llevan desde la matriz identidad hasta la matriz inversa de A.
Espero haberte ayudado.
-
Juan Daniel Fontalvo Rivas
el 29/11/16tengo este siguiente ejercicio, en estos momentos estoy dando el tema de derivada , quien me puede ayudar
Juan Daniel Fontalvo Rivas
el 29/11/16 -
Alberto Universidad
el 29/11/16Buenas noches, me he quedado enganchado con este problema porque no se muy bien como plantearlo:
Calcular el área entre las curvas y= a cos x e y=sen x eje OX entre 0 y pi/2. Nota: a es un número real positivo
Gracias anticipadas por la ayuda
