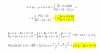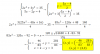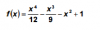-
Es cierto que el número de ecuaciones implicitas de un subespacio vectorial es igual a la dimension del espacio vectorial menos la dimension de subespacio?
Entonces, si yo trabajo en R3 y mi subespacio tiene una dimension 3, no lo puedo expresar en forma implicita?
comment


Antonio Silvio Palmitano
el 27/11/16Recuerda que un espacio vectorial es subespacio de sí msmo. Por lo tanto, si tienes el espacio vectorial R3, cuya dimensión es 3, y tienes un subespacio (S) de él de dimensión 3, resulta: S = R3. luego, expresamos formalmente: S = {<x,y,z> ∈ R3}, sin ecuaciones implícitas, ya que las componentes del vector genérico son independientes unas de otras.
Espero haberte ayudado.
-
1. Obtén las ecuaciones parametricas de la recta (r) que pasa por P (3,-2) y es perpendicular la recta 2x-y+4=0
2. Halla la ecuación implícita de la recta que pasa por (s) P(1,2) y por el punto de corte de las rectas r1:x-2y+3=0 y r2:2x+y+1=0
Ayuda por favor no se resolver estos dos ejercicios


Antonio Silvio Palmitano
el 27/11/161) Puedes plantear el vector director de la recta r: u = <a,b>, cuyas componentes debemos determinar.
Luego, puedes plantear la ecuación continua (o simétrica de la otra recta, tienes:
2x - y + 4 = 0, haces pasajes de términos y queda:
2x = y - 4, haces pasaje de factor como divisor y queda:
x = (y - 4)/2, que también puedes escribir en la forma:
(x - 0)/1 = (y - 4)/2, luego tienes el vector director: v = <1,2>.
Luego, como las rectas son perpendiculares, tenemos que sus vectores directores son perpendiculares y el producto escalar entre ellos es igual a cero, y planteamos:
u • v = 0, sustituimos las componentes de los vectores:
<a,b> • <1,2> = 0, desarrollamos el producto escalar:
a + 2b = 0, de donde despejamos y queda: a = - 2b,
luego, expresamos al vector director:
u = <a,b> = <-2b,b> = b<-2,1>, por lo que tenemos que el vector: u = <-2,1> (o cualquier múltiplo escalar no nulo de él) es un vector director de la recta r.
Luego, pasamos a las ecuaciones cartesianas paramétricas de la recta r:
x = 3 - 2t
y = -2 + t
t ∈ R:
2) Comencemos por plantear el sistema de ecuaciones para encontrar el punto de corte entre las rectas r1 y r2:
x - 2y + 3 = 0, de donde despejamos: x = 2y - 3 (*)
2x + y + 1 = 0
luego sustituimos en la segunda ecuación y queda:
2(2y - 3) + y + 1 = 0, distribuimos, reducimos términos semejantes y queda:
5y - 5 = 0, de donde despejamos: y = 1 (**),
luego reemplazamos en la ecuación señalada (*), resolvemos y queda: x = -1,
por lo que tenemos que la recta s pasa por el punto de corte: Q(-1,2).
Luego, con las coordenadas de los puntos P y Q, planteamos la pendiente de la recta s:
m = (2 - 2)/(-1 - 1) = 0/(-2) = 0.
Luego pasamos a su ecuación cartesiana, para lo que empleamos las coordenadas del punto P y la pendiente:
y - 2 = 0(x - 1), resolvemos el segundo miembro y queda:
y - 2 = 0, que es la ecuación cartesiana implícita de la recta s.
Espero haberte ayudado.

benson
el 1/12/16A partir de aquí no entendí ↓
<a,b> • <1,2> = 0, desarrollamos el producto escalar:
a + 2b = 0, de donde despejamos y queda: a = - 2b,
luego, expresamos al vector director:
u = <a,b> = <-2b,b> = b<-2,1>, por lo que tenemos que el vector: u = <-2,1> (o cualquier múltiplo escalar no nulo de él) es un vector director de la recta r.
Luego, pasamos a las ecuaciones cartesianas paramétricas de la recta r:
x = 3 - 2t
y = -2 + t
t ∈ R:
-
Alguien me puede ayudar a resolver esto, lo he intentado muchas veces y no me sale. Creo que me equivoco al sustituir que me queda la fracción al cuadrado y multiplicada por otro número. ES UN SISTEMA:
2x^2+3y^2=35
5x-2y=4


Antonio Silvio Palmitano
el 27/11/16Tienes el sistema de ecuaciones:
2x2 + 3y2 = 35
5x - 2y = 4, de donde puedes despejar: x = (4+2y)/5 (*),
luego sustituyes en la primera ecuación y queda:
2( (4+2y)/5 )2 + 3y2 = 35, desarrollamos el cuadrado en el primer término y queda:
2(16 + 16y + 4y2)/25 + 3y2 = 35, multiplicamos por 25 en todos los términos de la ecuación, distribuimos el primer término y queda:
32 + 32y + 8y2 + 75y2 = 875, hacemo, s pasaje de término, reducimos y ordenamos términos y queda:
83y2 + 32y - 843 = 0, cuyas soluciones son:
a) y = 3, luego reemplazas en la ecuación señalada (*), resuelves y queda: x = 2;
b) y = -281/83, luego reemplazas en la ecuación señalada (*), resuelves y queda: x = -46//83.
Luego, concluimos que el sistema tiene dos soluciones:
S1: x = 2, y = 3;
S2: x = -46/83, y = -281/83.
Espero haberte ayudado.
-
Buenas tardes. Tengo la siguiente duda.Si me piden volumen de revolucion, en torno al eje x y al eje y. Supongamos que la curva generatriz es y=x^2
La duda es:
Para hacer el volumen que gira en el eje x, el radio seria y=x^2 osea r=x^2?
Para el volumen que gira en torno al eje y, el radio seria x=raiz de y, osea r=raiz cuadrada de y?
Eso es lo que tengo un poco cruzado
-
Hola buenas, ¿Alguien podría ayudarme con este ejercicio que se me esta atravesando? Gracias de antemano.
Estudia el crecimiento y la curvatura de la siguiente función. Halla sus máximos, mínimos y puntos de inflexión:

Ángel
el 27/11/16Crecimiento/decrecimiento
1. Hacemos la primera derivada: f´(x)= -2x+(x3-x2)/2
2. Obtenemos las raíces de la primera derivada (puntos en los que se hace cero)
-2x+(x3-x2)/2=0------->2x=(x3-x2)/2-------->4x= x3-x2--------> x3-x2-4x=0------> x(x2-x-4)=0
x1=0, x2=(1+√17)/2, x=(1-√17)/2
3. Formamos intervalos representando en la recta real los valores de x1, x2 y x3
4. Tomamos un valor al azar (y a nuestra conveniencia)de cada intervalo y hallamos el signo que tiene en f´(x)....por ejemplo, para estudiar el intervalo [ (1+√17)/2, infinito)] lo lógico sería probar con calculadora o por tanteo que (1+√17)/2 es 2.56 y entonces sustituimos x=3 en f´(x)
Si f'(x) > 0 es creciente Si f'(x) < 0 es decreciente
-


Antonio Silvio Palmitano
el 27/11/16Llamemos:
x: cantidad de páginas diarias que lee Óscar, a: cantidad de días que tarda Óscar en leer la novela;
y: cantidad de páginas diarias que lee Bea, b: cantidad de días que tarda Bea en leer la novela;
z: cantidad de páginas diarias que lee Ainhoa, cantidad de días que tarda Ainhoa en leer la novela:
N: cantidad de páginas que tiene la novela.
Luego tenemos, a partir del enunciado:
x = y + 3 (Óscar lee diariamente tres páginas más que Bea),
y = z + 9 (Bea lee diariamente nueve páginas más que Ainhoa);
a = b - 1 (Óscar tarda un día menos que Bea en leer la novela),
b = c - 4 (Bea tarda cuatro días menos que Bea en leer la novela).
Luego, tenemos para la cantidad de páginas de la novela:
N = xa (cantidad de páginas diarias leídas por Óscar, multiplicada por la cantidad de días que tarda en leer la novela),
N = yb (cantidad de páginas diarias leídas por Bea, multiplicada por la cantidad de días que tarda en leer la novela),
N = zc (cantidad de páginas diarias leídas por Ainhoa multiplicada por la cantidad de días que tarda en leer la novela),
Luego, tienes el sistema de siete ecuaciones con siete incógnitas:
x = y + 3 (*)
y = z + 9, de donde despejas: y - 9 = z (**)
a = b - 1 (***)
b = c - 4, de donde despejas: b + 4 = c (****)
N = xa
N = yb (*****)
N = zc
Luego, sustituyes las expresiones señaladas (*) (**) (***) (****) (*****) en las demás ecuaciones y el sistema queda:
yb = (y + 3)(b - 1)
yb = (y - 9)((b + 4)
desarrollas los segundos miembros, cancelas términos y queda:
0 = - y + 3b - 3, de donde puedes despejar: y = 3b - 3 (******)
0 = 4y - 9b - 36
luego sustituyes en la segunda ecuación y queda:
0 = 4(3b - 3) - 9b - 36, distribuyes, reduces términos semejantes y queda:
0 = 3b - 48, de donde puedes despejar: b = 16;
luego reemplazas en la ecuación señalada (******), resuelves y queda: y = 45,
luego reemplazas en la ecuación señalada (*****), resuelves y queda: N = 720 (que es la respuesta que pide el enunciado del problema);
luego reemplazas en la ecuación señalada (****), resuelves y queda: 20 = c;
luego reemplazas en la ecuación señalada (***), resuelves y queda a = 15;
luego reemplazas en la ecuación señalada (**), resuelves y queda: 36 = z;
luego reemplazas en la ecuación señalada (*), resuelves y queda: x = 48.
Luego, concluimos que la obra tiene 720 páginas, y que:
Óscar leyó 48 páginas diarias y tardó 15 días en leerla,
Bea leyó 45 páginas diarias y tardó 16 días en leerla,
Ainhoa leyó 36 páginas diarias, y tardó 20 días en leerla.
Espero haberte ayudado.
-
En el vídeo de "Combinatoria: Permutaciones con repetición" sale como ejemplo un ejercicio el cuál dice "Formar números de 9 cifras con estos elementos: 222233344".
¿Son permutaciones con repetición porque se repiten los elementos (2 (4 veces), 3 (3 veces) , 4(2 veces)) o porque al crear la cifra de 9 dígitos podemos repetirlos?
¿Si el ejercicio fuera "Formar números de 9 cifras con los elementos siguientes: 123456789" seguiría siendo de permutación con repetición?