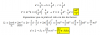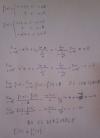-
miriam pino
el 21/11/16calcula las derivadas siguientes: El enunciado dice f(x)= (x3 +1)*e7x
Antonio Silvio Palmitano
el 21/11/16Observa que la función f resulta ser un producto, de la forma u*v, y en este caso tenemos:
u = x3 + 1, cuya derivada queda: u ' = 3x2,
v = e7x, cuya derivada queda: v ' = 7e7x;
Luego, aplicamos la regla de derivación de un producto de funciones:
f ' (x) = u ' * v + u * v ', sustituimos y queda:
f ' (x) = 3x2 * e7x + (x3 + ) * 7e7x.
Espero haberte ayudado.
-
miriam pino
el 21/11/16¿como puedo hacer la derivada de e7x?
lo que he hecho es e7x = f'(x)= e7x * 7e (estaría bien echo)
Gabriel
el 21/11/16
Antonio Silvio Palmitano
el 21/11/16 -
genesis
el 21/11/16 -
patricia
el 21/11/16tenia una pregunta, lo de reduccion al primer cuadrante en trigonometria en un ejercicio o problema como se pondria en practica, es decir, que te pueden pedir o preguntar? (tengo el examen el jueves, si me puedes responder antes seria genial)gracias!
-
Jean Piers Atoche Herrera
el 21/11/16
por favor ayuda con esto
David
el 21/11/16Se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado, pero no olvidéis de adjuntarlo de forma LITERAL, para saber que os piden. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-
Pablo
el 21/11/16Buenas, tengo una duda en un problema con polinomios ya que no sé resolverlo y me entrará en examen.Dice así:
El diámetro de la base de un silo cilíndrico mide 3/4 de la longitud de la altura.
-
a) Expresa la capacidad del silo en función del diámetro de su base.
-
b) Queremos pintar el silo y empleamos 1 kg de pintura por cada m2. ¿Cuántos Kg de
pintura se necesitan si el diámetro de la base mide 2 m?
Si alguien sabe cómo se hace se lo agradecería
-
-
Denise serra sanchez
el 21/11/16hola chicos necesito ayuda
2. Un polinomio de tercer grado tiene 5 como coeficiente de x³ y las raíces de este polinomio son 2, -2 y 1. ¿Cuál es este polinomio?Gabriel
el 21/11/16Aquí tienes alguna ayuda.
Transforma las raíces en binomios, que sería (x-2), (x+2) y (x-1). Multiplica los tres binomios y te saldrá una ecuacion de tercer grado x3.
Ahora como tendrás un polinimo que será del tipo x3+ax2+bx+c, multiplica por 5 a todos los sumandos para que te dé el polinomio que te pide del tipo 5 x3+5bx2+5bx+5c
Espero que te sea útil.
Saludos.
-
Denise serra sanchez
el 21/11/16hola chicos necesito ayuda
1. Considera els polinomis P(x)=x4 - 2x2 +1 i Q(x)= x2 - 7x + 3. Calcula P(x) – Q(x) i simplifica el resultatado.
-
jose
el 21/11/16hola unicoos que tal? me podrian ayudar con la siguiente integral?
∫x^2 - 1/x^3 - 2x^2 -5x +6
a mi me termina dando -->1/5 ln (x+2) + 4/5 ln (x-3) - 4/5 ln (x-1)
Gabriel
el 21/11/16 -
Ángel
el 21/11/16Hola,
tengo este ejercicio resuelto:
Y yo lo hice así:
¿Es igualmente válida esta forma de resolverlo?
¿Para razonar la no derivabilidad habría que decir que porque "no coinciden las derivadas laterales", porque "no son un número finito" o ambas razones?
Gracias
