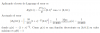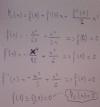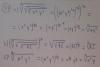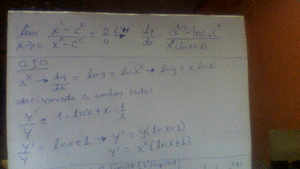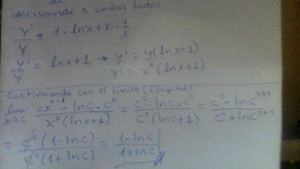Siempre trataremos de maximizar la expresión g(s) del coeficiente en el resto, para acotarlo.

Si la expresión es decreciente (como en este ejercicio), tomaremos el extremo del intervalo con menor valor absoluto.

Si la expresión es creciente, tomaremos el extremo con mayor valor absoluto.

Espero haberte ayudado.

¿y en este caso por qué se toma un punto intermedio (el 1/2) para calcular el error?

Me piden obtener P₂ en a=0 de f(x)= -x⁵/60 + x⁴/24 y aproximar el valor en f(1)

Observa que el centro de desarrollo es 0, y que el punto de cálculo es 1.

Observa que la expresión de la derivada tercera queda:

f⁽³⁾(x) = - x² + x, luego evaluamos: f⁽³⁾(c) = - c² + c, con 0 ≤ c ≤ 1.

Luego, si estudias la función: g(c) = - c² + c, verás que alcanza un máximo absoluto en c = 1/2, y que al evaluarla queda: g(1/2) = 1/4 (observa que g(0) = 0 y g(1) = 0).

Este es un caso en que la expresión g(c) no corresponde a un función estrictamente creciente o estrictamente decreciente, por lo que es necesario encontrar el valor de c para el que toma su valor máximo en valor absoluto.

Luego, la expresión del resto de Lagrange queda:

R(x) = (- c² + c)/3! x³ = (- c² + c)/6 x³ , con 0 ≤ c ≤ 1.

Luego, pasamos a la acotación:

| R(x) | = |(- c² + c)|/6 |x|³ , luego evaluamos para x = 1 y queda:

| R(1) | = |(- c² + c)|/6 , luego, como la expresión g(c) = - c² + c, alcanza su valor máximo para c = 1/2, con g(1/2) = 1/4, tenemos:

| R(1) | ≤ (1/4)/6 = 1/24.

Espero haberte ayudado.

Gracias.

Teorema de Rouche

Rubén va 

Puedes plantear la sustitución (cambio de variable):

w = √(x), de donde tienes. dw = dx / 2√(x), de donde despejas y tienes: 2dw = dx/√(x), luego sustituyes y la integral queda:

I = ∫ dx / ( √(x)•cos²√(x) ) = 

=  ∫ 2dw / cos²w = 2 ∫ dw / cos²w =

= 2tan(w) + C = 2tan( √(x) ) + C.

Espero haberte ayudado.

Por favor, dirige tu consulta al Foro de Física para que los colegas puedan ayudarte.

Foto del enunciado original, por favor.

Espero haberte ayudado :D, saludos.

Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas

Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)

Holas

Cuando multiplicas (a+3)3, le pones a + 9 en lugar de de 3a + 9 ( en el primer Ruffini).

Espero haberte ayudado saludos :D

Mil Gracias! Ya entiendo que debo tambien multiplicar las letras. Ahora haciendo las correcciones desde el punto que marcaste y cambiando los valores tanto para a como para b; me quedarian estas ecuaciones que no me permiten anular ninguna letra para continuar con el ejercicio.  3b+9a=12

                    b+a=-10

-----------------------------------------

                4b+10a=2                          Sera que no estoy haciendo los pasos correctos para resolver este tipo de ejercicios?

Observa bien cuáles son las informaciones que tienes en el enunciado:

1) (x-3) es divisor, lo que corresponde a que 3 es raíz, y por lo tanto tienes: P(3) = 0 (*).

2) P(1) = 24 (**).

Luego, evaluamos según las condiciones señaladas (*) (**) y queda el sistema de ecuaciones:

27 + 9a + 3b - 15 = 0

1 + a + b - 15 = 24,

hacemos pasajes de términos en ambas ecuaciones, y el sistema queda:

9a + 3b = - 12

a + b = 38,

dividimos por 3 en todos los términos de la primera ecuación y queda:

3a + b = - 4

a + b = 38,

resuelves el sistema y su solución es: a = - 21, b = 59.

Luego, la expresión del polinomio queda:

P(x) = x³ - 21x² + 59x - 15.

Luego, como sabemos que 3 es una raíz, dividimos con la Regla de Ruffini:

       1    -21    59   -15

3              3   -54     15

       1    -18      5      0

Luego, el cociente queda:

C(x) = x² - 18x + 5,

y puedes calcular sus raíces por medio de la fórmula resolvente para ecuaciones polinómicas cuadráticas (te dejo la tarea).

Espero haberte ayudado.

para completar el ejercicio :v las raices te deben quedar x=9 + 2√19 , x=9 - 2√19 , espero haberte ayudado xD :,v

Saludos!!!

Hola!! Gracias por toda la ayuda. Si llegue a esas raices con ayuda de una calculadora ya no he dado nada sobre radicales. Busque informacion en internet y aprendi como trabajarlos al menos para este ejercicio. De igual forma no entiendo como hacer la factorizacion del polinomio (x^3-21x^2+59) con este resultado ya que las raices no son exactas.

Sera correcto solo poner (x-3)(x-9 + 2√19)(x+9 - 2√19)?