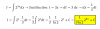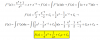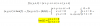-
Juan
el 9/11/16 -
Andres Perez Sala
el 9/11/16Buenas, me podéis ayudar con este ejercicio
gracias
Antonio Silvio Palmitano
el 9/11/16Observa que la matriz A tiene tres filas y tres columnas, la matriz B tiene dos filas y tres columnas, y la matriz X debe tener dos filas y tres columnas, ya que en la ecuación matricial se suma la matriz X con la matriz B. Luego, llamamos I a la matriz identidad de tres filas y tres columnas, y comenzamos con la ecuación matricial de enunciado:
X + B = XA, hacemos pasajes de términos y queda:
X - XA = -B, multiplicamos por la matriz identidad de orden tres en el primer término por la derecha:
XI - XA = -B, extraemos factor común por la izquierda:
X(I - A) = -B, multiplicamos por la derecha en ambos miembros por la matriz inversa de (I - A):
X(I - A)(I - A)^(-1) = -B(I - A)^(-1), resolvemos el producto entre matrices inversas:
XI = -B(I - A)^(-1) = resolvemos a la izquierda y llegamos a:
X = -B(I - A)^(-1).
Luego debes calcular las matrices -B e (I - A)^(-1) y efectuar el producto.
Espero haberte ayudado.
-
aylen
el 9/11/16 -
Tiza
el 9/11/16Hola buenas tardes, pueden ustedes ayudarme con este ejercicio. Espero que me puedan ayudar con él, siento las molestias causadas. Gracias y un saludo. (He realizado el apartado a), pero no el apartado b)) P.D. Está planteado pero no sé si es así, el b no se como hacerlo. Por favor ayudad me.
-
Michael
el 9/11/16Hola queria saber si me pueden ayudar con este problema. Me pide encontrar f(x) y me da como dato la segunda derivada f''(x)=(x^4+1)/x^3 Por favor si pueden ayudarme le agradeceria muchisimo porque no entiendo como hacerlo
-
Alex Domínguez
el 9/11/16Hola, me ayudan con estos ejercicios de algebra lineal ? Quiero saber como se haría la primera imagen , y si en la siguiente imagen están bien hechos los ejercicios
Gracias de antemano
-
Esleyder
el 9/11/16
Me pueden ayudar con este problema de circuitos lógicos? Se tiene una palabra de 5 bits, los últimos 4 bits representan un digito BCD, el primero es un bit de paridad impar (que significa esto, aclarenmelo porfa). Obtenga la tabla de la verdad y el pama de Karnaugh de las funciones siguientes: b).- F1 Se hará 1 para palabras con paridad incorrecta. Ok, mi duda no es que me resuelvan todo, lo que me pasa es que no entiendo a lo que el problema se refiere en lo que puse entre paréntesis. Y eso de palabras de paridad incorrecta, ni idea de que es. F2 supongo que se refiere a los valores de salida de la tabla de la verdad.
-
Manu
el 9/11/16Buenos días.
Si algún unicoos puede ayudarme.
En la inecuación 5x/2 +1 < 3x/7 -2 me dice que el resultado es X < - 42/29 pero mi resultado da X < - 3/30
Gracias.
Antonio Silvio Palmitano
el 9/11/16Para comenzar, puedes multiplicar en todos los términos de la inecuación por 14 (que es el mínimo común múltiplo entre los denominadores), observa que como es un factor positivo no altera el sentido de la desigualdad, lo haces y queda:
35x + 14 < 6x - 28, haces pasajes de términos y queda:
35x - 6x < -14 - 28, resuelves en ambos miembros y queda:
29x < - 42, divides en ambos miembros por 29, que como es un divisor positivo no altera el sentido de la desigualdad, y llegas a:
x < -42/29.
Espero haberte ayudado.
-
Gean Franco
el 9/11/16Hola buenas, quería saber si alguien me puede ayudar con este problema, lo he intentado pero no logro resolverlo. Solo se que hay que usar el método de Biseccion o el de Newton. Gracias!
-
I'm a your worse nightmare
el 9/11/16Hola buena, solo quería saber si me podeís ayudar, se que es con el teorema de bolzano que dice que si una función en un intervalo cerrado [a,b] y toma valores de signo contrario en los extremos, entonces existe c para el (a,b) tal que f(c)=0. Creo que es con este teorema, pero no se si sirve. Gracias y un saludo
Antonio Silvio Palmitano
el 9/11/16Observa que una de las hipótesis del Teorema de Bolzano es que la función debe ser continua en el intervalo cerrado, que se cumple según el enunciado. Luego tienes que el intervalo cerrado es [-1,1], y que f(-1) = f(1), pero observa que no se cumple la segunda hipótiesis, que es que f(-1) y f(1) tengan signos distintos.
Luego, definimos una nueva función, con dominio [0,1], y con la expresión: g(x) = f(x) - f(x-1), y observa:
la función g es continua en el intervalo cerrado [0,1] porque es resta entre funciones continuas en dicho intervalo;
luego evaluamos la nueva función en los extremos del intervalo:
g(0) = f(0) - f(0-1) = f(0) - f(-1) = a
g(1) = f(1) - f(1-1) = f(1) - f(0) = < recuerda que tenemos f(1) = f(-1) > = f(-1) - f(0) = -a,
por lo tanto la función g toma valores opuestos (por lo tanto con signos distintos) en los extremos del intervalo y,
como se cumplen las hipótesis del Teorema de Bolzano, tenemos que existe c ∈ (0,1),tal que:
g(c) = 0, reemplazamos la expresión de la función g evaluada y queda:
f(c) - f(c-1) = 0, hacemos pasaje de término y llegamos a:
f(c) = f(c-1).
Espero haberte ayudado.
