Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

Joship
el 26/10/16

Como puedo despejar para que me dé la tradicional formula de la varianza en el apartado II)

••0 voto/s
•
Antonius Benedictus
el 26/10/16
Va:

•0 voto/s
•

Cancelar
Rubén
el 26/10/16

Hola unicoos, por favor me podrían ayudar con este ejercicio de rectas normales y tangentes? cuando pone la ecuación de la recta normal...por qué pone x-e=0, no debería ser y-e=0?

••0 voto/s
•
César
el 26/10/16
Lo pone por que son paralelas a los ejes coordenados.

•0 voto/s
•
César
el 26/10/16
A ver si asi lo ves

•0 voto/s
•

Cancelar
Juli Ramos Monge
el 26/10/16

••0 voto/s
•
David
el 28/10/16
Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. Lo siento de corazón… Espero lo entiendas

•0 voto/s
•

Cancelar
Sebastian
el 26/10/16

Hola unicoos buenas tardes! Me podrian ayudar con este ejercicio? Debería hacer Gauss? Me he bloqueado un poco. Muchas gracias

••0 voto/s
•
César
el 26/10/16
Para abreviar te digo las operaciones sobre la matriz y como quedaría

•0 voto/s
•

Cancelar
Javier Rosado
el 26/10/16

Hola muy buena a tod@s unicoos!! Tengo un par de limites que por mas que lo intento, me superan..

Se supone que hacerlos por l'hopital es una locura, por ello he intentado hacerlos por infinitesimos, pero nada.

Si podéis ayudarme.. os lo agradecería un montón, muchas gracias!!!.

un saludo!

••0 voto/s
•
Antonius Benedictus
el 26/10/16
Podemos ayudarte, Javier:

•1 voto/s
•

Cancelar
Usuario eliminado
el 26/10/16

queria saber porque racionalizando 3√2/2√2 + 1 da 12-3√2/7, cuando yo lo calculo me da de resultado 6√2-3√2/7
graciasss

••0 voto/s
•
Ángel
el 26/10/16

•1 voto/s
•
Desencadenado
el 26/10/16

•1 voto/s
•

Cancelar
Pablo Reyes
el 26/10/16

Hola buenas tardes, mañana tengo examen de Algebra Lineal y bueno, me he atascado con este ejercicio. El apartado 1 lo tengo resuelto y sé que está bien porque lo he comprobado con otros compañeros pero el apartado 2 ninguno sabemos hacerlo :/ A ver si nos pueden echar una mano, les estaríamos muy agradecidos.

••0 voto/s
•
Antonius Benedictus
el 26/10/16
Va, Pablo:

•1 voto/s
•

Cancelar
Facundo Meier
el 26/10/16

Me pueden ayudar con este ejercico por favor,?. La consigna es hallar la concavidad y los puntos de inflexión de la función
x<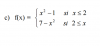Lo que hice fue derivar por partes y me quedó: 2x si x<=2 y 7 si 2<=x. Esto es igual a f¨(X)
f¨(X)= {2 si x<=2 y 0 si 2<=x
Ahora por criterio de la Derivada Segunda:
- Busque el punto crítico: x=2
- Analize la función en los intervalos: (-inf, 2) ; (2,inf)
- (-inf,2): f(0)=0 y en el intervalo (2, inf): f¨(3)=0
Por lo tanto la función siempre es concava hacia arriba
Muchas gracias

••0 voto/s
•
Antonio Silvio Palmitano
el 26/10/16
Observa que la función es continua en R, y particularmente en el punto de corte x= 2. Luego, la expresión de su derivada primera queda:
f ' (x) =
2x si x < 2
no está definida para x = 2 (observa que la derivadas laterales no coinciden)
-2x si x > 2 (observa que toma valores negativos en todo el intervalo, por lo que tienes que f es decreciente en (2,+inf)
Observa que el primer trozo se anula para x = 0, que corresponde a su intervalo, por lo que es un punto crítico, luego evaluamos f ' ' (0) = 2 > 0, lo que nos indica concavidad hacia arriba, y que f presenta un mínimo en x = 0.
Observa que el segundo trozo se anula para x = 0, pero no corresponde a su intervalo.
Observa que la derivada primera no está definida para x = 2, por lo que lo consideramos un punto crítico.
Luego observemos el comportamiento en cada intervalo:
(-inf,0): f es decreciente,
x = 0: mínimo,
(0,2): f es creciente,
x = 2: máximo,
(2,+inf): decreciente.
Luego, la derivada segunda queda:
f ' ' (x) =
2 si x < 2 (observa que es constante positiva, por lo que ya tienes que f es cóncava hacia arriba en el intervalo (-inf,2)
no está definida para x = 2 (observa que f presenta inflexión en x = 2
-2 para x > 2. (observa que es constante negativa, por lo que ya tienes que f es cóncava hacia abajo en el intervalo (2,+inf).
Luego, puedes ayudarte con un gráfico (resulta la unión de dos tramos de parábolas), y puedes corroborar los resultados que obtuvimos.
Observa también que la gráfica presenta un "punto anguloso" o "pico" en el punto (2,3), que resulta ser un punto máximo y también un punto de cambio brusco de concavidad.
Espero haberte ayudado.

•1 voto/s
•

Cancelar
José Rodríguez Lomeña
el 26/10/16

Sean u, v, w tres vectors linealmente independentes de un espacio vectorial E. Demostrar que u + v, u + w, v + w son linealmente independentes.

••0 voto/s
•
Pablo Reyes
el 26/10/16
Lo son, mírate estos vídeos. https://www.youtube.com/watch?v=L9K2YzLlNYQ
https://www.youtube.com/watch?v=H_hGlOBnoaA
https://www.youtube.com/watch?v=KwFTld4jFP4

•0 voto/s
•
Antonio Silvio Palmitano
el 26/10/16
Tienes que u, v, w son linealmente independientes, por lo tanto (indicamos vector nulo con N):
au + bv + cw = N con a=b=c=0 (*).
Luego, planteamos la combinación lineal nula para los vectores u+v, u+w, v+w (A, B, C son números reales cuyos valores debemos determinar):
A(u + v) + B(u + w) + C(v + w) = N, distribuimos los productos de escalar por suma de vectores en cada término:
Au + Av + Bu + Bw + Cv + Cw = N, ordenamos términos:
Au + Bu + Av + Cv + Bw + Cw = N, extraemos factor común vectorial por grupos de dos términos:
(A + B)u + (A + C)v + (B + C)w = N, luego, por la ecuación señalada (*) tenemos:
a = A+B = 0, b = A+C = 0, c = B+C = 0, y los tres vectores (u+v, u+w, v+w) resultan ser linealmente independientes.
Espero haberte ayudado.

•1 voto/s
•

Cancelar