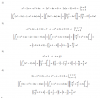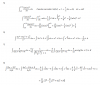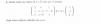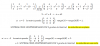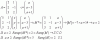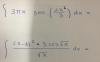-
AYUDA POR FAVOR
REPRESENTA GRÁFICAMENTE, APLICANDO TRASLACIONES, LA SIGUIENTE FUNCIÓN Y DETERMINA SU DOMINIO, RECORRIDO, MONOTONÍA Y SIMETRÍA:
F(X)=I X-2 I


Breaking Vlad
el 24/1/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-
Alguien podría explicarme estos ejercicios paso a paso, le tengo que explicar a mi hijo y de verdad agradecería mucho que me ayudaran.
-


David
el 29/1/20Hola! Me encantaría ayudarte, pero no respondemos dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
 4ºESO. Sistema inecuaciones con 1 incógnita.
4ºESO. Sistema inecuaciones con 1 incógnita.Buenas noches. ¿Le echáis un vistazo al adjunto ejercicio por favor? Apostaría que la solución es ∅, pero no estoy seguro del todo.
El intervalo de la inecuación a es (-6, 0) y el de la inecuación b es [0, -∞). ambas parece que comparten el eje Y, pero es sólo aparente, ya que dicho eje Y es únicamente parte de la inecuación b. Por favor comentar.
-