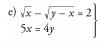Con esos datos, es imposible que f(3)=1.

Tienes la ecuación:

z³ = -2 + 2*√(3)*i (1).

Luego, observa que en el segundo miembro de la ecuación señalada (1) tienes al número complejo, expresado en forma cartesiana binómica:

w = -2 + 2*√(3)*i, que pertenece al segundo cuadrante,

cuyo módulo es (te dejo los cálculos): |w| = 4,

y la tangente de su argumento es: tanφ = 2*√(3)/(-2) = -√(3), compones con la función inversa de la tangente, y queda:

φ = 2π/3 rad = 120°;

luego, con el módulo y el argumento, expresas a este número complejo en forma polar, y queda:

w = 4_2π/3 (2).

Luego, sustituyes la expresión señalada (2) en el segundo miembro de la ecuación señalada (1), y queda:

z³ = 4_2π/3, extraes raíz cúbica en ambos miembros, y queda:

z = ∛(4_2π/3), aplicas la Fórmula de De Moivre para las raíces de un número complejo, y queda:

z_k = ∛(4)_{(2π/3 + 2*k*π)/3}, con k = 0, 1, 2 (3),

que es la expresión general de las tres soluciones de la ecuación de tu enunciado;

luego, evalúas la expresión general señalada (3), y queda:

z₀ = ∛(4)_(2π/9) = ∛(4)_(40°),

z₁ = ∛(4)_(8π/9) = ∛(4)_(160°),

z₂ = ∛(4)_(14π/9) = ∛(4)_(280°),

que son las tres soluciones de la ecuación de tu enunciado, expresadas en forma polar (módulo-argumento).

Espero haberte ayudado.

Por favor, intenta conseguir el enunciado que motiva tu problema y envía una foto del mismo, para que podamos ayudarte.

EJERCICIO 3

EJERCICIO 4

EJERCICIO 5

x,- edad del padre hoy,  y.- edad de la hija hoy:

La edad del padre tiene el triple de la edad de su hija :     x = 3y

Hace 10 años (el padre tenía x - 10 y la hija  y -10 ) el padre tenía 7 veces la edad de su hija:    x - 10 = 7 (y - 10)

Resolviendo por sustitución el sistema formado por las dos ecuaciones anteriores, resulta:     3y - 10 = 7y -70  de donde   4y = 60  entonces  y = 15  y  x = 45.

EL PADRE TIENE 45 AÑOS Y LA HIJA 15.

Muchas gracias

Tienes el número complejo expresado en forma binómica:

w = -√(2)/2 + [√(2)/2]*i, que pertenece al segundo cuadrante,

cuyo módulo es (te dejo el planteo): |w| = 1,

y la tangente de su argumento es: tanθ = [√(2)/2]/(-√(2)/2) = -1, por lo que su argumento es: θ = 3π/4 rad = 135°;

luego, con los valores del módulo y del argumento que tienes remarcadas, expresas a este número complejo en forma polar, y queda:

w = 1_3π/4 (1).

Luego, tienes la expresión de tu enunciado:

z = ∛( -√(2)/2 + [√(2)/2]*i ), sustituyes la expresión señalada (1) en el argumento de la raíz cúbica, y queda:

z = ∛( 1_3π/4 );

luego, aplicas la Fórmula de De Moivre para las raíces de un número complejo, y queda:

z_k = (∛[1])_{(3π/4+2*k*π)/3}, con k = 0, 1 o 2,

aquí resuelves la expresión del módulo, y queda:

z_k = 1_{(3π/4+2*k*π)/3}, con k = 0, 1 o 2 (2),

que es la expresión general de las raíces cúbicas del número complejo: w = -√(2)/2 + [√(2)/2]*i;

luego, evalúas la expresión señalada (2), y tienes las expresiones polares de las tres raices cúbicas

z₀ = 1_π/4 = 1_45°,

z₁ = 1_11π/12 = 1_165°,

z₂ = 1_19π/12 = 1_285°;

luego, expresas a las tres raíces en forma trigonométrica, y queda:

z₀ = 1*(cos[π/4] + i*sen[π/4]) = 1*(cos[45°] + i*sen[45°]),

z₁ = 1*(cos[11π/12] + i*sen[11π/12]) = 1*(cos[165°] + i*sen[165°]),

z₂ = 1*(cos[19π/12] + i*sen[19π/12]) = 1*(cos[285°] + i*sen[285°]);

luego, reemplazas los valores de las expresiones trigonométricas, distribuyes, y queda:

z₀ = √(2)/2 + [√(2)/2]*i ≅ 0,707 + 0,707*i,

z₁ ≅ -0,966 + 0,259*i,

z₂ ≅ 0,259 - 0,966*i,

que son las expresiones de las tres raíces cúbicas en forma cartesiana binómica.

Queda que hagas el gráfico correspondiente.

Espero haberte ayudado.

Tienes el número complejo expresado en forma binómica:

w = -4/(1 - √[3]*i), multiplicas al numerador y al denominador por el conjugado de este último, y queda:

w = -4*(1 + √[3]*i) / ([1 - √[3]*i]*1 + √[3]*i), resuelves el denominador, y queda:

w = -4*(1 + √[3]*i)/4, simplificas, distribuyes el signo, y queda:

w = -1 - √[3]*i, que pertenece al tercer cuadrante,

cuyo módulo es (te dejo el planteo): |w| = 2,

y la tangente de su argumento es: tanθ = -√[3]/(-1) = √[3], por lo que su argumento es: θ = 4π/3 rad = 240°;

luego, con los valores del módulo y del argumento que tienes remarcadas, expresas a este número complejo en forma polar, y queda:

w = 2_4π/3 (1).

Luego, tienes la expresión de tu enunciado:

z = ⁴√( -4/(1 - √[3]*i) ), sustituyes la expresión señalada (1) en el argumento de la raíz cuarta, y queda:

z = ⁴√( 2_4π/3 );

luego, aplicas la Fórmula de De Moivre para las raíces de un número complejo, y queda:

z_k = ⁴√[2]_{(4π/3+2*k*π)/4}, con k = 0, 1, 2 o 3 (2),

que es la expresión general de las raíces cuartas del número complejo: w = -4/(1 - √[3]*i)i;

luego, evalúas la expresión señalada (2), y tienes las expresiones polares de las cuatro raíces cuartas

z₀ = ⁴√[2]_π/3 = ⁴√[2]_60°,

z₁ = 1_5π/6 = ⁴√[2]_150°,

z₂ = 1_4π/3 = ⁴√[2]_240°,

z₁ = 1_11π/6 = ⁴√[2]_330°.

Espero haberte ayudado.