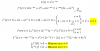-
Arnau Planas
el 23/11/17Buenas tardes, ¿podrían ayudarme con este ejercicio de funciones? Muchas gracias.
f(x)= x2 e-ax cuando a es distinto a zero.
a) calcular el valor de a para que esta función tenga un extremo relativo en el punto de abcisa x=2
b) Cuando a=2, clasificar los extremos relativos.
-
Miguel Gallego
el 23/11/17 -
Bet
el 23/11/17 -
Maria
el 23/11/17Hola buenos dias, necesito ayuda con el problema 1 a y 1 b, por favor! Muchas gracias
Antonio Silvio Palmitano
el 24/11/171b)
Tienes la ecuación: cosx = x, haces pasaje de término, y queda:
cosx - x = 0,
luego, observa que en el primer miembro tienes la expresión de una función continua en R:
f(x) = cosx - x,
luego, evalúas para x = 0 y para x = π/2, y tienes los valores:
f(0) = cos(0) - 0 = 1 > 0,
f(π/2) = cos(π/2) - π/2 = 0 - π/2 = - π/2 < 0,
luego, por el Teorema de Bolzano tienes que existe c ∈ (0,π/2) tal que:
f(c) = 0, sustituyes la expresión del primer miembro, y queda:
cos(c) - c = 0, haces pasaje de término, y queda:
cos(c) = c.
Espero haberte ayudado.
-
johan ayala
el 23/11/17
-
Sr.M
el 23/11/17Buenas, alguien podría explicarme esta integral por otro método por favor. Es que sigo sin entenderlo.
Antonius Benedictus
el 23/11/17No hay otro método. Para funciones racionales como la que aparece, es necesario descomponer la en "fracciones parciales".
Integral racional en fracciones simples 01 y siguientes.También:
http://www.apuntesmareaverde.org.es/grupos/mat/Bachillerato/BC2%2010%20Integrales.pdf
-
Rubén
el 23/11/17Hola, ¿me pueden explicar por qué ℤ no es cuerpo? Por lo que he buscado es porque no existe el inverso de un número entero tal que a*(1/a)=1, pero si por ejemplo se coge a=-1, sustituyendo en lo anterior: (-1)*(1/(-1))=1 por lo que si se cumple la propiedad del inverso y ¿Z sí sería cuerpo no?
-
Marest
el 23/11/17Me pueden ayudar por favor? Muchas gracias
Compramos un rollo de cable telefónico y usamos las siete novenas partes. Sabiendo que aún nos quedan 88 metros, ¿Cuál era la medida inicial del rollo?
-
Anthony Andujar
el 23/11/17En una anterior pregunta nadie entendio, veran este ejercicio esta resuelto pero el profesor me dijo que lo tengo que desglosar y sacar otros cálculos porque esta todo Directo el ejercicio y el lo quiere paso a paso .
