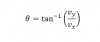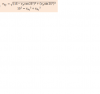-
Francisco Gutiérrez Mora
el 9/12/16Buenas Tardes Francisco Javier:
Te pediría por favor que mirases la resolución del ejercicio que planteó Carlos Manuel Lopo, pues basándonos en los mismos argumentos, no nos sale a ambos la misma Vo. Un Saludo.
Francisco Gutiérrez Mora
el 10/12/16Muchísimas gracias por tu ayuda. He leído por ahí abajo un comentario diciendo que eres lo mejor de este foro de física: pues efectivamente es así, lo comparto y lo corroboro. No hay nadie hasta ahora que te haya hecho sombra Francisco Javier. Créeme, lo que te digo no es un cumplido es una realidad palpable. Muchas gracias amigo. Es usted una gran persona que ayuda mucho a los demás que lo necesitan. Mis Saludos y respetos.
Francisco Gutiérrez Mora
el 10/12/16 -
Mer
el 9/12/16Si representas una gráfica de la Ec, Ep y Em del péndulo frente al ángulo de oscilación, ¿ qué forma debe tener estas gráficas?
Lucía
el 9/12/16Si situamos las energías en el eje Y y el ángulo del péndulo en el eje X
La energía mecánica sería una línea paralela al eje de las x, pues siempre es la misma.
La energía cinética a mi modo de ver sería una línea recta también, pues está en constante movimiento.
La energía potencial sería una parábola.
Francisco Javier
el 10/12/16En los extremos donde llega el péndulo, la energía cinética es cero pero la energía potencial es máxima. En cambio cuando el péndulo pasa por su posición de equilibrio su energía cinética es máxima pero su energía potencial es cero. Si soltamos el péndulo con una inclinación inicial desde el reposo, la gráfica para la energía cinética tendría forma de una parábola invertida y la gráfica para la energía potencial tendría forma de una parábola. La energía mecánica del sistema sería una línea recta que empieza y termina desde los extremos máximos de la energía potencial, cortando en el punto máximo de la energía cinética. Te dejo un bosquejo en la siguiente imagen.
-
Alex Domínguez
el 9/12/16Una cosa amigos, hoy en una resolución de Francisco Javier me surgieron dos dudas, que son mas bien matemáticas diría yo pero las pongo aquí acorde a que son de física
En el módulo de la magnitud de Vbf, como conseguiste simplificar desde ese término a √2vo,
La otra es , de donde sale el término de donde consigues sacar el ángulo, es decir, esto
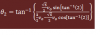
Muchas Gracias !! Un abrazo !
Francisco Javier
el 9/12/16Lo de la magnitud del vector Vbf sale al efectuar las operaciones pertinentes. Puede parecer que no, pero sin contar a Vo, todo lo que está dentro de la raíz son números. Te invito a comprobarlo. Para la dirección de un vector, en este caso Vbf, siempre será válida la ecuación plasmada en la imagen de abajo si se tiene las componentes rectangulares de dicho vector, lo cual es el caso para este problema. Ahora el que te pide un favor soy yo. Para la próxima trata de plasmar las dudas que tengas en la pregunta original. Así evitamos acumulación de preguntas con el mismo tema.
Alex Domínguez
el 9/12/16Alex Domínguez
el 9/12/16 -
Ronny Molina Pereira
el 9/12/16me he pasado horas tratando de hallar la respuesta me ayudan por favor
nunca habia hecho un ejercicio con 3 sustancias
Alex Domínguez
el 9/12/16Ronny Molina Pereira
el 9/12/16 -
Manu
el 9/12/16Buenos días
Aquí muestro un ejercicio donde al intentar aplicar los valores a la formula no me daría ninguno de los ejemplos del ejercicio.
Francisco Javier
el 9/12/16
Manu
el 9/12/16Buenos días.
Lo cierto es que no he dormido hoy pero, no sé, parece que, cuando el proyectil toca el suelo: el cos45, no le saco esos 12,606. Si pudieras explicarlo por favor. Y otra cosa, si lo realizo ccn gravedad 10 m/s^2, los demás resultados, no saldrían acordes con los resultados propuestos o, es que, sensillamente, tu prefieres trabajar con gravedad 9,8 ?
Saludos Cordiales
Ángel
el 9/12/16
Francisco Gutiérrez Mora
el 9/12/16
Francisco Gutiérrez Mora
el 9/12/16
Francisco Javier
el 9/12/16
Francisco Gutiérrez Mora
el 10/12/16 -
Alex Domínguez
el 8/12/16Hola, como se haría este ejercicio ? ME estoy liando mucho, si puede ser hagánlo planteando y relacionando las ecuaciones de la Energía cinética ya que se conserva y la del momento lineal p, que habría que pasarlo a coordenadas polares creo, muchas gracias
Yo he llegado a plantear estas dos ecuaciones, si llamamos A a la bola pequeña y b a la grande
Vbf= √[(3Voa - √5Vfa*cosθa)2 + (√5Vfa*Senθa)2/ 22]
Esta a partir del momento lineal,
Vbf = √[(3Voa)2 - (√5 Vfa)2 / 2 ]
esta a partir de la ocnservación de al energía cinética
Creo que me falta por conseguir el ángulo pero no se como hacerlo, decidme si está bien planteado ,como sería su resolución con estas ecuaciones y el resultado, muchas gracias de verdad !
Quiero aclarar que la primera raíz es a partir del módulo, y la segunda a partir de que Vbf está elevado a dos porque ne la fórmula de la energía cinética es elevada a 2
Francisco Javier
el 9/12/16 -
Alex Salazar
el 8/12/16Me pueden ayudar con este ejercicio para saber como ocupar las formulas de velocidad angular y si tengo que sacar la frecuencia
-
Alex Domínguez
el 8/12/16Hola Francisco, es una parte de una resolución de un p`oblema de Francisco Javier, que suele estar mucho aquí y es muy bueno, hay que considerar que Vf y Va es la misma, subo su resolución, lo que no terminé de coger fue ese sistema
El sistema es lo que no he conseguido sacar, gracias
Francisco Javier
el 9/12/16 -
Alex Domínguez
el 8/12/16 -
Manu
el 8/12/16Buenos días.
Aquí no sé aplicar la trigonometría.
gracias
