-
Hola, pido ayuda a los profesores Antonio y César .He intentado hacer la siguiente integral por dos métodos diferentes. Con el método de integración por partes, la desarrollo aplicando la regla ALPES para asignar u pero llego a otra integral por partes y no sé qué hacer. Por cambio de variable o sustitución, la tengo mal porque no sé desarrollar. No la hagan de nuevo, solo díganme, ya sea por escrito o en una foto, cuál es el fallo y cómo se procede. Muchas gracias!


-
ayuda para resolver esta identidad
tga/tg2a-tga=cos2a

manuelfr99
el 29/10/16Hola Marina. La resolución de esta igualdad es muy sencilla, por tanto, te indicaré los pasos a seguir a continuación.
1. Desarrola tg 2a y realiza la operación del denominador (tg 2a - tg a). Ten en cuenta que tg 2a ha de estar simplificada.
2. Una vez que hayas operado, te quedará una fracción así: (1-tg2 a)/(1+tg2 a). Expresa las tangentes en función de senos y cosenos y llegarás al resultado pedido.
-
Como se calcula el argumento de estos complejos.
Z= 3(Cos 3/4 pi + isen 3/4pi)
A)Arg(Z^4)?.. En este caso creo que tengo que poner 4*3/4pi + 2kpi pero no se si el 4 multiplica al 2kpi tambien o como es la simplificacion.
B) Arg ( z / | z | )
C) Arg | z / | z | |
Los demas de mi guia de matematica ya los resolvi pero estos seiran los mas dificiles que no entiendo.


Antonio Silvio Palmitano
el 29/10/16Para calcular el argumento de una potencia debes aplicar la Fórmula de De Moivre: Arg(z^n) = n*Arg(z) para el argumento principal, y sumar 2kpi para el argumento general.
a) Arg(z^4) = 4*(3/4)pi = 3pi, luego como excede a 2pi: Arg(z^4) = 3pi - 2pi = pi (argumento principal).
Luego observa que el módulo de z es un número real positivo al que, al expresarlo como un número complejo, le corresponde argumento igual a cero.
b) Aplicas la propiedad del argumento de una división:
Arg(z/|z|) = Arg(z) - Arg(|z|) = (3/4)pi - 0 = (3/4)pi (argumento principal).
c) Observa que el módulo del cociente entre z y el módulo de z es igual a uno:
| z/|z| | = propiedad del módulo de un cociente = |z|/| |z| | = observa que el módulo de z es un número real positivo
= |z|/|z| = 1 (observa que 1 es un número real positivo, por lo que tenemos que su argumento es 0).
Luego
Arg(| z/|z| ) = Arg(1) = 0.
Con respecto a este último ejercicio:
observa que z es un número complejo, y su módulo se expresa: |z|;
observa que |z| es un número real positivo, por lo que su módulo es igual a su valor absoluto, que coincide con él: | |z| | = |z|.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 29/10/16Observa que se ha aplicado la sustitución (cambio de variable):
w = x^2, cuyo diferencial queda: dw = 2x*dx.
Observa que en el miembro central de la igualdad han multiplicado por 1/2 y por 2, para poder aplicar la sustitución, vamos con el desarrollo:
Integral ( x * e^(x^2) * dx ) = multiplicamos por 1/2 y por 2:
= (1/2) * Integral ( 2x * e^(x^2) * dx ) = ordenamos factores en el argumento de la integral:
= (1/2) * Integral ( e^(x^2) * 2x*dx ) = aplicamos la sustitución:
= (1/2) * Integral ( e^w * dw ) = resolvemos:
= (1/2) * e^w + C = sustituimos:
= (1/2) * e^(x^2) + C.
Espero haberte ayudado.
-
Hoola! No entiendo la solución de esta integral resuelta, ¿no se supone que podemos separarla en dos integrales? ¿qué pasa con la raíz de x que está fuera? Gracias
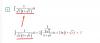


Antonio Silvio Palmitano
el 29/10/16Otra vez se aplicó un cambio de variable, en este caso:
w = 1 + V(x), cuyo diferencial es dw = ( 1 / (2V(x)) )*dx,
y en el desarrollo han multiplicado por 2 y por (1/2), vamos con los pasos:
Integral ( 1 / ( V(x)*V(1+x) )*dx = multiplicamos por 2 y por 1/2
= 2 * Integral ( 1 / ( 2*V(x)*V(1+x) )*dx = expresamos el argumento de la integral como producto de fracciones:
= 2 * Integral ( ( 1/(2V(x)) ) * ( 1/V(1+x) ) ) * dx = ordenamos factores en el argumento de la integral
= 2 * Integral ( ( 1/V(1+x) ) * ( 1/(2V(x)) ) * dx = aplicamos el cambio de variable:
= 2 * Integral ( 1/w ) * dw = resolvemos:
= 2 * ln|w| + C = aplicamos el cambio de variable:
= 2 * ln| 1 + V(x) | + C.
Espero haberte ayudado.






















