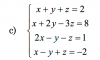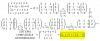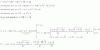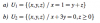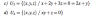Pon el enunciado Sara

El sistema es compatible:

Te explicamos, Alejandro:

Va Jordi , la ultima es trivial

Por favor, indica cuáles son los enunciados, para que podamos ayudarte.

Cuales de los subconjuntos anteriores de R3 son subespacios

Ninguno. Un subespacio está caracterizado por un sistema de una o más ecuaciones lineales HOMOGÉNEAS:

Si te fijas, en el primero no está el vector nulo.

Y en el segundo, el opuesto de (0,0,5) no está, pero sí el (0,0,5).

Antonio, como siempre, muchas gracias de veras. 

Entendí tu explicación para el primer apartado pero en el segundo no mucho. Un subespacio no ha de cumplir?: 

 1. La suma de elementos del conjunto también está dentro del conjunto

 2. Un escalar con dominio en un cuerpo de operadores K con la ley.c.externa multiplicado por un elemento del conjunto es también solución...

Luego el elemento opuesto (inversible) al que tu refieres no lo entiendo. Un abrazo

Es lo que has escrito al final para el valor k=-1.

Ah vale vale, ya lo entendí! entonces por la misma razón estos dos tampoco son subespacios verdad?

El primero, sí, pues son DOS ecuaciones lineales homogéneas (una recta vectorial o cápsula lineal).

El segundo, no.

No tiene sentido operar con logaritmos si no son ecuaciones, pero bueno...

Mírate estos vídeos para entender mejor los logaritmos:

 
http://www.unicoos.com/leccion/matematicas/1-bachiller/sucesiones-y-limites/logaritmos

Que vaya bien el examen.

1) x = (a+b)^3 / ( 3*V(2) ), planteamos logaritmos en ambos miembros:

logx = log( (a+b)^3 / ( 3*V(2) ) ), aplicamos propiedad del logaritmo de un cociente:

logx = log( (a+b)^3 ) - log( 3*V(2) ), aplicamos propiedad del logaritmo de una potencia, y del logaritmo de un producto:

logx = 3*log(a+b) - ( log3 + log(V(2)) ), distribuimos el signo en el agrupamiento, y aplicamos propiedad del logaritmo de una raíz:

logx = 3*log(a+b) - log3 - (1/2)*log(2).

2) y = 1/V(8), planteamos logaritmos en ambos miembros:

logy = log( 1/V(8) ), aplicamos propiedad del logaritmo de un cociente:

logy = log1 - log(V(8)), resolvemos el primer término, y aplicamos propiedad del logaritmo de una raíz en el segundo término:

logy = 0 - (1/2)*log(8), expresamos a 8 como potencia de 2 y cancelamos término nulo:

logy = - (1/2)*log(2^3), aplicamos porpiedad del logaritmo de una potencia:

logy = -(1/2)*3*log2, resolvemos factores racionales:

logy = - (3/2)*log2.

Recuerda cuáles son las propiedades que hemos aplicado:

log1 = 0 

log(a*b) = loga + logb

log(a/b) = loga - logb

log(a^p) = p*loga

log( (rV)(a) ) = (1/r)*loga (indicamos raíz de índice r como (rV)).

Espero haberte ayudado.

Te lo demostramos, Pablo:

Pablo, aplica algo similar al ejercicio de arriba.

Muchas gracias por tu labor Antonio, siempre estás ahí para echarme un cable a mí y a muchos otros. lo que haces pero no está pagao' ! Mis respetos.

Te lo explicamos, Daniel:

Va una orientación, queda si es preciso para que realices las operaciones entre las matrices.

1°) Observa que la matriz nula: O perteneciente a R^(2*2) verifica:

A*O = O y también O*A = O.

Observa que si consideramos dos matrices B1 y B2 que pertenecen al conjunto, tenemos:

A*B1 = B1*A (*) y A*B2 = B2*A (**)

2°) Luego, verificamos que la matriz duma B1+B2 pertenece al conjunto:

A*(B1 + B2) = distribuimos = A*B1 + A*B2 = aplicamos las igualdades (*) y (**) = B1*A + B2*A  = extraemos factor común por derecha = (B1 + B2)*A.

3°) Luego, verificamos que el múltiplo escalar de una matriz del conjunto pertenece al conjunto: sea k perteneciente a R, y la matriz B1 perteneciente al conjunto, que cumple: A*B1 = B1*A (*). luego planteamos para la matriz k*B1:

A*k*B1 = ordenamos factores, según propiedades del producto de matrices por escalares = k*A*B1 = aplicamos la igualdad (*) = k*B1*A.

Luego, por las tres condiciones que se cumplen, tenemos que el conjunto es un subespacio de R^(2*2).

Espero haberte ayudado.