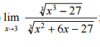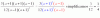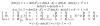-
DueFreitas
el 11/10/16Profe la del medio me vuelve loco, se la sabe ?
Emilio Lopez
el 11/10/16 -
YANET
el 11/10/16hola me podrían ayudar con este ejercicio es que lo hice pero cuando hago la comprobación no me da el resultado así que supongo que está incorrecto, gracias.
i=n
Se considera : ∑(2i- 1)(2i + 1) = an(4n² + 6n – 1)
i= 1
Hallar a para que la igualdad se cumpla para n=2.
TENGO HECHO ESTO Y ME DIO a = 3, PERO CUANDO HAGO LA COMPROBACIÓN NO ME RESULTA.
(2X1- 1)(2X1 + 1) + (2X2-1) (2X2+1) = a.2 (16+12 -1)
3+15 = 18 = 2a(27) →54a
54 a = 18
a= 54/18→ a = 3
-
pedro
el 11/10/16Hola, alguien podría decirme como se resuelve el limite de una raiz cubica cuyo radicando es una fracción? Gracias!!
-
lbp_14
el 11/10/16Hola Unicoos, tengo que simplificar esta fracción pero tengo las soluciones y no me sale, lo de arriba es lo que he hecho y la solución la de abajo, podrían ayudarme o decir en qué me he equivocado?
Mil gracias.
lbp_14
el 11/10/16 -
Lau
el 11/10/16Hola alguien podría ayudarme con este ejercicio llevo ya tiempo haciéndolo pero me atasco a la mitad, os lo agradecería mucho. Muchas gracias
Antonio Silvio Palmitano
el 11/10/16Primero expresemos a los argumentos de las raíces como potencias o productos de potencias:
9 = 3^2
12 = 2^2 * 3
6 = 2*3
Luego expresemos a cada factor como potencia con exponente fraccionario.
Los factores en el numerador (N) quedan:
( 3^2 )^(1/3) = propiedad de las potencias cuyas bases son otras potencias = 3^(2 * 1/3) = 3^(2/3)
( 2^2 * 3 )^(1/4) = propiedad distributiva = (2^2)^(1/4) * 3^(1/4) = 2^(2 * 1/4) * 3^(1/4) = 2^(1/2) * 3^(1/4)
Luego el numerador queda:
N = 3^(2/3) * 2^(1/2) * 3^(1/4) = ordenamos y aplicamos propiedad del producto de potencias con bases iguales =
= 2^(1/2) * 3^(2/3 + 1/4) = 2^(1/2) * 3^(11/12).
El denominador (D) queda:
D = (2*3)^(1/2) = 2^(1/2) * 3^(1/2).
Luego, reconstruimos la expresión fraccionaria:
N/D = ( 2^(1/2) * 3^(11/12) ) / ( 2^(1/2) * 3^(1/2) ) = simplificamos =
= 3^(11/12) / 3^(1/2) = aplicamos propiedad de las divisiones de potencias con bases iguales =
= 3^(11/12 - 1/2) = 3^(5/12).
Espero haberte ayudado.
-
Víctor López
el 11/10/16 -
Alejandro Ballesteros
el 11/10/16 -
Nico
el 11/10/16hola buenas tardes, tengo una duda sobre un ejercicio que tengo que resolver donde me piden que calcule un producto interno para el cual los vectores (1/4, 0) y (0, 1/2) sean una base ortonormal.. me podrian ayudar? mas que nada con una explicacion de como hacerlo porque tengo mas ejercicios similares y es fundamental que logre comprender lo que hago y no mecanizarme , desde ya se agradece la ayuda!
-
smorenobaware
el 11/10/16Buenos Dïas,
Me pueden ayudar a resolver el problema 11 de la figura anexa por favor
Antonio Silvio Palmitano
el 11/10/16Buscamos establecer relaciones pitagóricas entre las longitudes de los catetos (base y altura) y las longitudes de las hipotenusas correspondientes, en algunos triángulos rectángulos, por lo que debes ir dibujando segmentos durante el planteo del problema.
En el triángulo rectángulo superior de la izquierda tienes (llamamos A a la longitud de su hipotenusa):
(2x)^2 + 3^2 = A^2 (*).
Luego, traza un segmento vertical desde el extremos derecho del segmento de longitud 3 cm hasta cortar a la base de la figura (cuya longitud es 11 cm), y te queda determinado a su derecha un triángulo rectángulo cuya base mide: (11 - 3) cm = 8 cm, y su altura mide: x + 2x = 3z, luego para este triángulo (llamamos B a la longitud de su hipotenusa) tienes:
(3x)^2 + 8^2 = B^2 (**).
Luego, traza un segmento diagonal desde el vértice inferior derecho y el extremo superior del segmento vertical de longitud x de la izquierda, observa que es la hipotenusa (C) de un triángulo rectángulo cuya base mide 11 cm, y su altura mide x, luego para este triángulo tienes:
x^2 + 11^2 = C^2 (***)
Por último, observa que con los segmentos A, B y C ha quedado determinado otro triángulo rectángulo, y para él tenemos:
A^2 + B^2 = C^2
Luego, sustituimos según las expresiones que tenemos en las ecuaciones señaladas (*) (**) (***) y queda
(2x)^2 + 3^2 + (3x)^2 + 8^2 = x^2 + 11^2
Resolvemos potencias en cada término y queda:
4x^2 + 9 + 9x^2 + 64 = x^2 + 121
Hacemos pasajes de términos y queda
4x^2 + 9x^2 - x^2 = 121 - 9 - 64
Reducimos términos semejantes y queda:
12x^2 = 48
Dividimos por 12 en ambos miembros y queda:
x^2 = 4
Extraemos raíz cuadrada en ambos miembros (observa que x expresa una longitud) y queda:
x = 2.
Espero haberte ayudado.
-
Usuario eliminado
el 11/10/16Me pueden ayudar con el siguiente ejercicio, gracias.
Imagen adjunta
Antonius Benedictus
el 11/10/16Se trata de un determinante de "Vandermonde" (búscalo en Wikipedia)
Si pones x=2, comprobarás que obtienes dos columnas iguales. Lo mismo sucede con x = -3 y con x=4.
En los tres casos, el determinante vale 0, al haber dos columnas iguales.
Y no hay más soluciones, pues parece evidente que, si desarrollásemos este determinante, obtendríamos un polinomio de tercer grado.
