-
Claudias
el 1/10/16Utilice el polinomio de Taylor para hallar el valor aproximado
Antonio Silvio Palmitano
el 1/10/16Si has construido el polinomio de Taylor de grado 3, te ha quedado:
T(x) = -2(x - pi/2) + (4/3)(x - pi/2)^3
Luego, como debes aproximar empleando la función, tenemos:
sen(2x) = sen(pi + 0,1), comparamos argumentos:
2x = pi + 0,1, despejamos y queda:
x = p/2 + 0,05.
Luego planteamos la aproximación:
sen(2x) aprox T(x) = - 2(x - pi/2) + (4/3)(x - pi/2)^3, luego evaluamos:
sen(pi + 0,1) = T(pi/2 + 0,05) =
=- 2(pi/2 + 0,05 - pi/2) + (4/3)(pi/2 + 0,05 - pi/2)^3 =
= - 2*0,05 + (4/3)(0,05)^3 = - 0,099833 (aproximadamente).
Recuerda que para construir los coeficientes (Ai)del polinomio de Taylor asociado a la función, planteamos sus derivadas hasta el orden 3, y luego dividimos por el factorial correspondiente al orden:
f(x) = sen(2x), evaluamos: f(pi/2) = sen(pi) = 0, y tenemos: A0 = 0
f ' (x) = 2cos(2x), evaluamos: f ' (pi/2) = 2cos(pi) = -2, luego dividimos por 1! = 1 y queda: A1 = - 2
f ' ' (x) = - 4sen(2x), evaluamos: f ' ' (pi/2) = - 4sen(pi) = 0, y tenemos: A2 = 0
f ' ' ' (x) = - 8cos(2x), evaluamos: f ' ' ' (pi/2) = - 8cos(pi) = +8, luego dividimos por 3! = 6 y queda: A3 = 8/6 = 4/3.
Espero haberte ayudado.
-
Jordi García
el 1/10/16Buenos días,
¿alguien me puede ayudar en el siguiente ejercicio?
Es que lo resuelvo de distintas maneras y me dan resultados diferentes.
Gracias.
Antonio Silvio Palmitano
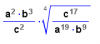
el 1/10/16Puedes comenzar por multiplicar y dividir convenientemente en el argumento de la raíz cuarta, para que queden factores con exponentes que sean múltiplos de 4 en el denominador, y expresas al numerador como producto de potencias:
c^17 / ( a^19 * b^9 ) = c^16 * c * a * b^3 / (a^20 * b^12) = ( c^16 / (a^20 * b^12) * a * b^3 * c.
Luego tomas raíz cuarta (la indicamos (4V)), simplificamos y distribuimos y queda:
(c^4 / (a^5 * b^3) ) * (4V)(a * b^3 * c)
Luego, multiplicamos por el factor racional que aún no hemos considerado y queda:
( a^2 * b^3 / c^2 ) * (c^4 / (a^5 * b^3) ) * (4V)(a * b^3 * c) = simplificamos factores racionales:
= (c^2 / a^3) * (4V)(a * b^3 * c).
En este tipo de expresiones, operamos para expresarla con denominador racional, y para que el factor irracional que pueda quedar en el numerador tenga potencias con exponentes estrictamente menores que el índice de la raíz.
Espero haberte ayudado.
-
Paula
el 1/10/16Hola, podrían explicarme este ejercicio:
Dada la función f(x)= 3x+2/x-1, calcula f^-1 (2) sin hallar la función inversa. ¿Puede hacerse lo mismo con f^-1(3)?
Gracias.
Antonio Silvio Palmitano
el 1/10/16Observa que teneos: f^(-1)(y) = x si y solo si y = f(x) (*).
Y si la expresión de la función es: f(x) = (3x + 2)/(x - 1), tenemos:
En el primer caso, sabemos que y = 2, reemplazamos en la ecuación señalada (*) y queda:
2 = (3x + 2)/(x - 1), hacemos psaje de divisor como factor:
2(x - 1) = 3x + 2, distribuimos a la izquierda:
2x - 2 = 3x + 2, hacemos pasajes de términos y reducimos términos semejantes:
- x = 4, de donde tenemos finalmente: x = - 4, y concluimos:
f^(-1)(2) = - 4.
En el segundo caso, sabemos que y = 3, reemplazamos en la ecuación señalada (*) y queda:
3 = (3x + 2)/(x - 1), hacemos psaje de divisor como factor:
3(x - 1) = 3x + 2, distribuimos a la izquierda:
3x - 3 = 3x + 2, hacemos pasajes de términos y reducimos términos semejantes:
0 = 5, que es una identidad absurda,
por lo que concluimos 3 no pertenece al dominio de la función inversa de f (o sea: f^(-1) no está definida para 3).
Espero haberte ayudado.
-
Samuel
el 1/10/16 -
andrea
el 1/10/16hola, queria saber como es la solucion de esta raiz: h^2= 18 *raiz cuadrada
de 6, perdona pero tan poco sé como poner raiz cuadrada con el teclado.un saludo
-
shadowreal
el 1/10/16
podrias hacer un video de binomios de newton tipo : {(29) + (29)} x 4!{(3 ) (25)} --------------------------630
Buenos días :
esque no entiendo muy bien como se hace la parte de los numeros sin fraccion y la de la exclamacion no se si me entenderas por que no tengo los carácteres necesarios para escribirlos pero bueno muchas gracias por toda la labor que estas haciendo por ayudarnos tanto
Antonio Silvio Palmitano
el 1/10/16 -
claudia nuñez ramirez
el 1/10/16
Buenas noches David, primero quiero felicitarte por tu dedicación y bella labor, y a la vez agradecerte por haberme dado una luz cuando estaba a punto de rendirme y a través de un compañero de carrera, (actualmente soy estudiante de segundo año de pedagogía en Matemáticas en la Universidad Austral de Chile) llegue a tus vídeos, realmente me salvaron el ramo (análisis matemático en una variable real AMUVAR ) .
Imagino que debes estar lleno de consultas y que posiblemente las respuestas se demoren un tiempo, pero he buscado vídeos de acerca de convergencia de series ( criterio de la raíz, de series p, de alternadas, de comparación, de leibniz, del cociente o de D'Alembert, series telescópicas, entre otras y no he podido encontrar en la página, en realidad es lo único que hasta el día de hoy no manejo bien acerca del ramo. Bueno te cuento que el profesor dio una tarea que será calificada (para los que ahora están cursando el ramo y no han podido resolverla, me pidieron ayuda mis amigos y compañeros que reprobaron el ramo el año pasado) y es para este lunes a primera hora, el problema es que como no manejo bien el tema no se como ayudarlos y es por esto que recurro a ti, para saber si puedes resolver la tarea ( determinar una serie que converge condicionalmente, entonces para todo S perteneciente a los R puede re ordenarse los términos de la serie dada y obtener una nueva serie que converja a un valor S (en este caso S es igual al R.U.T sin el dígito verificador de cada uno de los alumnos), ellos deben probar este teorema encontrando la serie, la general y luego hacer el caso particular), o darme luces para ayudarlos, subir vídeos para que aprenda el tema, y en realidad como sugerencia para después vídeos (cuando tengas algo de tiempo ) acerca de los criterios de convergencia de series pero llevado a demostraciones y ejemplos enfocado en que para los que estudiamos Pedagogía en matemáticas debemos entender de donde vienen y manejar cada tema a la perfección para así explicar luego a nuestros alumnos de la mejor manera.Resulta que en estos momentos no soy capaz de ayudar a mis amigos porque no manejo el tema, y me encantaría hacerlo por lo que agradecería vídeos de la materia, demostraciones y ejemplos para aprender , o si ya hay guiarme para saber donde están, pero en este momento necesito ayuda urgente para salvar a estos alumnos, si no reprobaran el ramo por segunda vez :c y me sentiría terrible que habiendo yo aprobado el ramo no pueda ayudarlos, pero fue algo que nosotros no vimos en su momento.
seria ideal, que si puedes, lo subieras lo antes posible para así yo pueda aprender el tema y enseñarles a ellos (o que ellos mismos aprendan viendo el vídeo y así se suman mas unicoos) para que lo entiendan y hagan su tarea a tiempo.
Finalmente tengo que decirte que eres seco!!! de verdad te admiro, y tus frases con increíbles, el año pasado me motivaste y me diste la confianza que si practicaba y practicaba de seguro aprobaría y así ha sido desde entonces en todos mis ramos matemáticos ( de echo en este momento estoy estudiando y viendo vídeos de geometría analítica ), me has enseñado mucho y eso se agradece desde ya.
atenta a tus comentarios , estamos en contacto :)
David
el 3/10/16
claudia nuñez ramirez
el 7/3/18Gracias David, creeme que unicoos, tus videos y tu me ayudaron demasiado al inicio de mi carrera, muchas gracias por todo, hace mucho no entraba al sitio y esta espectacular todo, vi que tienes muchos videos más, así que comenzaré a verlos (los uso hoy para abrir la mente de mis estudiantes) lamentablemente como usuaria normal no tengo acceso a los exámenes, pero de igual mudo es de mucha ayuda, sigue creando videos y ayudando a miles de estudiantes, un abrazo y GRACIAS POR TODO ;)
-
juana
el 1/10/16Buenas noches , tengo una pregunta con respecto a este ejemplo , cuando resuelvo problemas como este por medio de esa tabla y cuando no ....
Antonio Silvio Palmitano
el 1/10/16Cuando trabajas con distribuciones binomiales, como en este caso con población tamaño n = 10, probabilidad favorable p = 0,3 y, por lo tanto probabilidad desfavorable q = 0,7, pueden pedirte que calcules (llamamos F(k) = p(x >= k) a cada valor de la tabla acumulativa), van como ejemplos:
P(x >= 5) = F(5) = 0,150 (que es el caso del enunciado, y lo buscas directamente);
van otros ejemplos:
P(x > 5) = P(x >= 6) = F(6) = 0,047
P(x < 5) = 1 - P(x >=5) = 1 - F(5) = 1 - 0,150 = 0,850
P(x <= 5) = 1 - P(x > 5) = 1 - P(x >= 6) = 1 - F(6) = 1 - 0,047 = 0,953
P(x = 5) = P(x >= 5) - P(x > 5) = P(x >= 5) - P(x >= 6) = F(5) - F(6) = 0,150 - 0,047 = 0,103
P( 3 <= x <= 6) = P(x <= 6) - P(x < 3) = y resuelves cada término como hemos hecho en los ejemplos.
Espero haberte ayudado.
-
Reinel Rodriguez
el 1/10/16 -
Julio J Grimán
el 1/10/16
