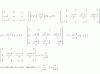F2+F3 queda -z=2... de donde z=-2... 
No puedes hacer determinantes, te dice que lo hagas por GAUSS
Con ese valor, si haces F1+F2 te quedará... x+by+(b-1).z=2... Como z=-2... x+by+(b-1).(-2)=2... x+by-2b+2=2... x+by=2b...
Y si tomas la ecuacion ax+ay=1, tendrás un sistema de dos ecuaciones con dos incognitas que no te debería ser dificil de DISCUTIR...
Te sugiero... Discutir un sistema - Método de GAUSS

Bueno yo lo hice así 

¿¿?? Lo siento, no entiendo.. 

hola!

Si solo estás en el conjunto de los números Reales entonces no se puede factorizar porque su discriminante es negativo..

pero si estás con complejos entonces haces este procedimiento

en donde la factorización sería (x+(3-3sqrt(3) i)/32)((x+ (3+3sqrt(3) i)/32) donde sqrt(3) es la raíz cuadrada de 3

Te lo demostramos, Mariam:

Si consideras al triángulo equilátero base, a partir de su centro puedes dibujar tres segmentos, cada uno con extremos en el centro C y en un vértice. Observa que te quedan tres triángulos isósceles, con dos de sus lados igual al radio  y el tercero igual a la longitud del lado del triángulo. Luego puedes plantear (l: lado del triángulo equilátero, observa que l = |u| = |v| = |u - v| = 4, r: radio del triángulo equilátero): 

l = 2r*cos30°, de donde tienes: l =V(3)*r, de donde puedes despejar: l/V(3) = r (*).

Luego, imagina el tetraedro regular: tiene cuatro caras triangulares equiláteras, y si consideras su altura h, ésta une el vértice V que no pertenece a la base con el centro de la misma. Observa también que las seis aristas del tetraedro tienen longitud l, y que si tomas uno de los vértices de la base, el centro C y el vértice V, te queda un triángulo rectángulo cuyos catetos son r y h, y su hipotenusa es l, por lo que puedes plantear la relación pitagórica y queda:

r^2 + h^2 = l^2, sustituimos según la ecuación señalada (*), resolvemos su término y queda:

(1/3)*l^2 + h^2 =l^2, hacemos pasaje de término, resolvemos a la derecha y queda:

h^2 = (2/3)*l^2, hacemos pasaje de potencia como raíz, distribuimos la raíz a la derecha y queda:

h = V(2/3)*l, reemplazamos l, resolvemos y queda:

h = 4*V(2/3).

Luego, el volumen del tetraedro queda:

Vt = (1/3)*S*h

donde S es el área del triángulo equilátero base, que por propiedad del producto vectorial queda:

S = (1/2)*| u x v |.

Debes tratar de graficar para ir viendo todos los pasos con detalle.

Espero haberte ayudado.

Te sugiero repasar las definiciones y propiedades de la media, mediana y moda de una distribución discreta. La mediana es el valor central en la lista completa (en este caso el promedio entre los valores que ocupan los lugares 15° y 16°, que es 2). La media (o promedio) no necesariamente se ubica en el centro de la lista completa, sino que se ubica más cerca de los valores más repetidos, en este ejemplo la media es 59/30 = casi 2.

La lista completa de elementos (son treinta en total) es:

0 0 0 0 0 1 1 1 1 1 1 1 1 (*) 2 2 (**) 2 2 2 2 2 2 2 2 3 3 3 4 4 5  9, cuya suma es: 59.

La media (que se ubica en el lugar indicado (*)) =

= (suma de elementos)/(cantidad de elementos) = 59/30 = 1,967 (aproximadamente).

La mediana se ubica en el lugar señalado (**) =

= (valor central o, en este caso, promedio de los valores centrales) = (2 + 2)/2 = 4/2 = 2.

Observa que hay quince valores antes, y quince valores después de la mediana.

La moda es el valor más repetido, en este caso: 2.

Espero haberte ayudado.

Debes emplear las propiedades de los logaritmos (cuyos argumentos deben ser estrictamente positivos):

loga + logb = log(ab)

loga - logb = log(a/b)

log( a^p ) = p*loga

Vamos con uno de tus ejercicios a modo de ejemplo, así puedes continuar con los demás, para lo que te recomiendo recurras a los vídeos.

9) Indicamos logaritmo en base 5 como LOG:

LOG( x^2 + 21x - 10 ) - LOG( 5x - 1) = 2, aplicamos la segunda propiedad y queda:

LOG( (x^2 + 21x - 10)/(5x - 1) ) = 2, luego componemos con la función inversa del logaritmo en base 5 ( se llama exponencial en base 5, y su expresión es: 5^x) y queda:

(x^2 + 21x - 10)/(5x - 1) = 5^2, resolvemos a la derecha, hacemos pasaje de divisor como factor y queda:

x^2 + 21x - 10 = 25*(5x - 1), distribuimos a la derecha y queda:

x^2 + 21x - 10 = 125x - 25, hacemos pasajes de términos, reducimos términos semejantes a la izquierda y queda:

x^2 - 104x + 15 = 0, observa que es una ecuación polinómica cuadrática, aplicamos la fórmula resolvente y quedan las soluciones (aproximadas):

x1 = 103,86, que es solución porque con él se obtienen argumentos positivos para los logaritmos en la ecuación original,

x2 = 0,14, que no es solución, porque con él se obtiene un argumento negativo para el primer logaritmos en la ecuación original.

Recuerda que cuando no indican explícitamente la base de los logaritmos, consideramos que la base es 10.

Espero haberte ayudado.

Practicando y practicando:

Va otra:

División sintética o Ruffini

¿Me podría explicar?

Por favor, verifica la expresión que debes factorizar, ya que por lo que has escrito tendría dos variables: M y m.

La expresión esta escrita correctamente 

Oh es cierto, perdón seria: M5-2M2+6M

Planteamos:

M^5 - 2M^2 + 6M, extraemos factor común a la izquierda:

= M( M^4 - 2M + 6).

Luego, debemos verificar si la expresión del agrupamiento es factorizable, para lo que estudiamos si tiene raíces la función cuya expresión es:

y = x^4 - 2x + 6, planteamos su derivada primera y su derivada segunda:

y ' = 4x^3 - 2

y ' ' = 12x^2

Planteamos la condición de punto crítico (o singular): y ' = 0, sustituimos y queda:

4x^3 - 2 = 0, despejamos y queda ( indicamos raíz cúbica como (3V) ):

x = (3V)(1/2), evaluamos en la derivada segunda para estudiar la concavidad en el punto crítico:

y ' ' ( (3V)(1/2) ) =12*( (3V)(1/2) )^2 > 0, por lo que tenemos concavidad hacia arriba en el punto crítico, por lo que la función presenta un mínimo para x = (3V)(1/2).

Luego, evaluamos la expresión de la función para el punto crítico y queda:

y( (3V)(1/2) ) = ((3V)(1/2)) ^4 - 2((3V)(1/2)) + 6 > 0, por lo que tenemos que el valor mínimo de la función es positivo, por lo que todos sus demás valores son positivos, por lo que tenemos que la función cuya expresión es y = x^4 - 2x + 6 no presenta raíces.

Por lo tanto, la expresión factorizada queda: M(M^4 - 2M + 6).

Espero haberte ayudado.

MUCHÍSIMAS GRACIAS, es grande JAJA

¿¿?? ¿Y cual es tu duda?. Se trata de que hagas todas las operaciones...  Te sugiero estos vídeos.. Suma de fracciones con m.c.m

A partir de ahí, se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. #nosvemosenclase Nos cuentas ¿ok?