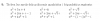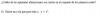En el caso de un límite de "e": la función "e" es  conocida por ser continua en todos los puntos de x, por lo que se saca  el límite de la función a la que está elevada "e" y luego se eleva "e" a este resultado.

En otras palabras, sacas el límite de (2/x) cuando 0 tiende a la izquierda, y luego elevas "e" a ese resultado. No se si se entendió bien.

Observa que estás tratando con el límite:

Lím(x-->0-) ( e^(2/x) ) = 

planteamos la sustitución (cambio de variable):

w = -2/x (observa que w tiende a +infinito cuando x tiende a cero por la izquierda), y al multiplicar por -1 en ambos miembros queda: -w = 2/x, luego el límite queda:

= Lím(w-->+inf) ( e^(-w) ) =

= Lím(w-->+inf) ( 1 / e^w ) = 0.

Observa que e^w tiende a + infinito, por lo que 1 / e^w tiende a cero.

Espero haberte ayudado.

AUB representa a todos los numeros de ambos intervalos, coincidan o no......  [-3,4]
A∩B representa solo a aquellos numeros que pertenecen a los dos intervalos a la vez.. (-1,3]
B-C son todos los elementos de B excepto los que pertenecen al C... [2,4]
Y C-B son todos los elementos del C, excepto los que pertenecen al B.... [-4,-1]
Para la próxima sería genial que al menos dibujases los intervalos en la recta real...

Teayudamos, Laura:

No puedes igualar a 0 parte del polinomio. 

Descompón el polinomio inicial por la regla de Ruffini.

Te va a quedar:  (x-3)(x+1)(2x-5)

Igualando a 0 cada factor, obtienes las tres raíces reales del polinomio:

x=3, x=-1  y x=5/2.

66) Vamos con la definición de continuidad de una función en un punto de su dominio:

1°) f(a) = 8

2°) Lím(x-->a) (x^2 - a^2)/(x - a) = factorizamos el numerador = Lím(x-->a) (x + a)(x - a)/(x - a) = simplificamos

= Lím(x-->a) (x + a) = 2a.

3°) 2a = 8, de donde obtenemos: a = 4.

34) Aplicamos regla de la cadena (observa que tienes una potencia cúbica, cuyo argumento consta de dos términos, y el segundo de ellos es una cuarta potencia cuyo argumento es un binomio de segundo grado):

g ' (x) = 3 * ( 2 + (x^2 + 1)^4 )^2 * ( 0 + 4 * (x^2 + 1)^3 * 2x ) (puedes seguir operando luego, pero la derivación ya terminó).

Espero haberte ayudado.

Para los dos primeros, tienes ecuaciones bicuadráticas:

1) (x^2)^2 + 4(x^2) + 3 = 0

luego aplicas la fórmula resolvente para ecuaciones cuadráticas, y tendrás dos opciones:

a) x^2 = -1, de donde despejas: x = V(-1) y tienes dos raíces: x1 = -i, x2 = i;

b) x^2 = -3, de donde despejas x = V(-3) y tienes otras dos raíces: x3 = -V(3)*i, x4 = V(3)*i.

2) (x^2)^2 + (x^2) + 1 = 0

luego aplicas la fórmula resolvente para ecuaciones cuadráticas, y tendrás dos opciones:

a) x^2 = -1/2 + V(-3/4) = -1/2 + (V(3)/2)*i (observa que el módulo es 1 y el argumento es 120°);

b) x^2 = -1/2 - V(-3/4) = -1/2 - (V(3)/2)*i (observa que el módulo es 1 y el argumento es 240°).

Luego, con la fórmula de las raíces de De Moivre que seguramente has visto en clase, tendrás dos raíces por cada opción, que en forma polar quedan:

a) x1 = (1)(60°), x2 = (1)(240°);

b) x3 = (1)(120°), x4 = (1)(300|°).

3) Tienes una ecuación cuadrática con coeficientes complejos, por lo que es más conveniente completar binomio elevado al cuadrado:

x^2 + 2i*x - V(3)*i = 0, hacemos pasaje de término:

x^2 + 2i*x = V(3)*i, sumamos i^2 en ambos miembros:

x^2 + 2i*x + i^2 = i^2 + V(3)*i, factorizamos a la izquierda y resolvemos el primer término a la derecha:

(x + i)^2 = -1 + V(3)*i, expresamos al complejo de la derecha en forma polar (observa: módulo 2, argumento 120°):

(x + i)^2 = (2)(120°), hacemos pasaje de potencia como raíz:

x + i = V( (2)(120°) ), aplicamos la fórmula de las raíces de De Moivre y tenemos dos opciones:

a)

x + i = ( V(2) )(60°), expresamos en forma trigonométrica a la derecha:

x + i = V(2) * (cos60° + isen60°), distribuimos y resolvemos a la derecha:

x + i = V(2)/2 + ( V(6)/2 )*i, hacemos pasaje de término y extraemos factor común y queda:

x1 = V(2)/2 + ( V(6)/2 - 1 )*i;

b)

x + i = ( V(2) )(240°), expresamos en forma trigonométrica a la derecha:

x + i = V(2) * (cos240° + isen240°), distribuimos y resolvemos a la derecha:

x + i = - V(2)/2 - ( V(6)/2 )*i, hacemos pasaje de término y extraemos factor común y queda:

x2 = - V(2)/2 - ( V(6)/2 + 1 )*i.

Espero haberte ayudado.

A cada entero positivo "n"  (que está en la habitación n) reúbicalo en la habitación "2n".

A cada entero negativo "- n" ubícalo en la habitación "2n+1", que ha quedado vacía.

El 0, en la 1ª habitación.

Sin el 0:

A cada n→2n-1

A cada  -n→2n.

Va, punk:

Muchas gracias por tu ayuda lo entendí y resolví todos los apartados 

Si, ambas son funciones continuas, y el dominio de la función producto es la intersección de los dominios de las funciones U y V.

Lo mismo ocurre con la suma, la resta y la composición de funciones continuas.

Espero haberte ayudado.

como son funciones de 2 variables, y obtuve las derivadas parciales, facatorizando llegue a una del tipo e^fx    y un polinomio. como el domino de las 2 es todo R^2. entonces se cumple lo que dijiste no?

Si, tal cuál. Es válido todo para funciones de dos, tres o n variables, siempre y cuando sean continuas.

No existe.

Puedes darte una idea al estudiar los límites para x tendiendo a +infinito y tendiendo a -infinito de la función cuya expresión es x^2:

Lím(x-->+inf) (x2) = +infinito

Lím(x-->-inf) (x^2) = +infinito

Por lo tanto tenemos que la función cuya expresión toma valores cada vez mayores a medida que x tiende a +infinito o a -infinito, por lo que no existe una cota superior para su imagen, por lo que no existe un número real y tal que, para todo x perteneneciente a los reales, y sea mayor que x^2.

Espero haberte ayudado.