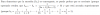No estoy nada convencido del método, pero por si te vale te lo dejo 

Disculpen la confusion pero el denominador el seno es solo del 3x no del -1

Va felipe es mas sencilla que la otra

En el primer término tenemos una potencia con base distinta de cero y exponente cero, por lo que su valor es 1, luego extraemos factor común en los últimos tres términos y queda:

1 + V(2) * ( - 3/4 + 1/2 - 1 ) = resolvemos en el agrupamiento = 1 + V(2) * (-3/4) = resolvemos y ordenamos factores en el segundo término = 1 - (5/4)*V(2) = 1 - 5*V(2) / 4.

Por lo tanto tu resultado es correcto.

Espero haberte ayudado.

Para tu primera pregunta, por favor envía el enunciado completo.

Para la segunda, debes distribuir, y recordar que i^2 = - 1:

(3+5i) (3 - 5i) = 3*3 - 3*5i + 5i*3 - 5i*5i = resolvemos en cada término = 9 - 15i + 15i - 25*i^2 = cancelamos términos opuestos, sustituimos i^2 =

= 9 - 25*(-1) = 9 + 25 = 34.

Espero haberte ayudado.

Por favor, revisa tus cálculos para el valor de a, porque es 12, y e valor de b es 11/6.

Observa que para el límite del segundo trazo (con x tendiendo a 2 por la izquierda) queda: 1/6 + b, y que el valor de la función para x = 2 queda: 2/a + b, luego para tener continuidad por la izquierda en x=2 planteamos:

2/a + b = 1/6 + b, cancelamos los sumandos iguales en ambos miembros y queda:

2/a = 1/6, hacemos pasajes de divisores como factores queda:

2*6 = 1*a, resolvemos y queda:

12 = a.

El valor para la constante b es correcto.

Espero haberte ayudado.

Te ponemos nuestro resultado. Revisa las operaciones, José:

Gracias por tomarse la molestia, son unos genios realmente

Pero me queda una duda

¿por que esta igualdad 2/a + b = 1/6 + b, esta relacionada con la continuidad por izquierda?

Te va la demostración, Víctor:

Debes tener en cuenta la identidad trigonométrica del coseno de la resta de dos ánguos, para el segundo miembro de la igualdad (indicamos theta como D):

A * ( cos(wt)*cosD + sen(wt)*senD ) = (distribuimos) = Acos(wt)*cosD + Asen(wt)*senD = ordenamos factores = AcosD*cos(wt) + AsenD*sem(wt).

Luego comparas con la expresión en el primer miembro y tienes:

a = AcosD

b = AsenD

Luego, si elevas al cuadrado en ambos miembro en ambas ecuaciones quedan:

a^2 = A^2 * (cosD)^2

b^2 = A^2 * (senD)^2

Luego sumamos miembro a miembro, extraemos factor común a la derecha y queda:

a^2 + b^2 = A^2 * ( (cosD)^2 + (senD)^2 ), luego por identidad trigonométrica pitagórica en el segundo factor de la derecha tenemos que:

a^2 + b^2 = A^2 * 1, resolvemos a la derecha, y luego hacemos pasaje de potencia como raíz y llegamos a:

V( a^2 + b^2 ) = A.

Espero haberte ayudado.

Observa los denominadores en las expresión del término general bn (b con subíndice n):

son todos de la forma n+k, con k = 1, 2, ... n, por lo que todos los valores de k son menores o iguales que n, por lo tanto tenemos:

n+k >= n, multiplicamos por 1 en ambos miembros y queda:

1*(n+k) >= 1*n, hacemos pasajes de factores como divisores y queda:

1/n >= 1/(n+k), y si leemos la desigualdad de derecha a izquierda tenemos que:

1/(n+k) <= 1/n, lo que indica que cada término de la expresión del término general bn es menor o igual que 1/n, por lo que tenemos:

bn = 1/(n+1) + 1/(n+2) + ... * 1/n <= 1/n + 1/n + ... + 1/n = (observa que son n términos) = n*1/n = 1.

Por lo tanto una cota superior es 1, que es lo que quieren mostrar en tu enunciado.

Espero haberte ayudado.

(√(14+√(7-4√81)))-½  = resolvemos la raíz cuarta de 81:

= (√(14+√(7-3)))-½    = resolvemos la resta:

=  (√(14+√(4))-½    = resolvemos la raíz cuadrada de 4:

= (√(14+2))-½    = resolvemos la suma:

=  (√(16))-½    = resolvemos la raíz cuadrada:

= (4)-½            = resolvemos la potencia (observa que es fraccionaria y con signo negativo):

= 1/2.

Espero haberte ayudado.
                         

Recuerda la identidad trigonométrica:

( secA )^2 = 1 + ( tanA )^2.

Obsrva que has olvidado la constante arbitraria de integración en las dos soluciones que has propuesto.

A partir de la primera solución general (agregamos la constante arbitraria):

I = (1/4) * ( sec(2x) )^2 + C = aplicamos la identidad tirgonométrica:

= (1/4) * ( 1 + ( tan(2x) )^2 ) + C = distribuimos en el primer término:

= 1/4 + (1/4) * ( tan(2x) )^2 + C = ordenamos términos y asociamos términos constantes:

= (1/4) * ( tan(2x) )^2 + ( 1/4 + C ) = observa que como C es una constante arbitraria, tenemos que 1/4 + C = K es también una constante arbitraria, y queda:

= (1/4) * ( tan(2x) )^2 + K (observa que hemos obtenido la segunda solución, pero con la constante arbitraria de integración sumada).

Por lo tanto, hemos mostrado que las dos soluciones son equivalentes, hecho que ocurre muy frecuentemente con las identidades trigonométricas.

Espero haberte ayudado.

HOLA ERICK TE AYUDO

Si defines matrices semejantes como aquéllas que tienen el mismo rango, la misma traza y los mismos autovalores, lo son. 

Si no, mira el documento adjunto:

O sea que depende de la definición que se le de?

La definición clásica es la que te he puesto. Lo que sucede es que algunos textos también se refieren como "semejantes·" a las matrices que tienen el mismo rango.

En un espacio vectorial puedes definirse un producto interno (o producto escalar) que es una forma bilineal, simétrica, no degenerada y definida positiva. Esto es, el producto escalar es conmutativo, homogéneo, distributivo respecto la suma, no hay vectores no nulos ortogonales a todos y ¡el producto escalar de un vector por sí mismo es siempre no-negativo, y vale 0 si se trata del vector nulo!. Pues bien, se define una Norma (o módulo) del siguiente modo: La raíz cuadrada positiva de su cuadrado escalar, i.e., del producto escalar del vector por sí mismo. Y a partir de ahí, se crea una Métrica....