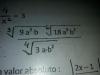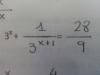Responde esta pregunta...

Hola mira lo que tienes que hacer es poner la matriz aumentada y la llevas a la forma escalonada por renglones

Responde esta pregunta...

Gracias! Lo queria hacer por cramer, pero por gaus me resulto mas rapido.

Responde esta pregunta...

Responde esta pregunta...

Como el límite de la suma es la suma de los límites, si tienes dos sucesiones de S, la suma de ambas debería también pertenecer a S. Pero la suma de ambas tiene por límite 2a. Entoncres:

2a=a

a=0.

De este modo también si multiplicamos una sucesión de S por un escalar, resulta otra sucesión con límite 0.

Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. Lo siento de corazón… Espero lo entiendas

Ya no importa,lo entiendo... gracias por responder ,por sus videos y su amabilidad!! 

Como el binomio (2x^4 - 3) divide a q(x), tienes que es uno de sus factores.

Como el grado del polinomio q(x) es 5, planteamos un producto con un binomio de grado 1:

q(x) = (2x^4 - 3)(ax + b).

Luego, aplicamos el Teorema del Resto:

q(-1) = -1(-a + b) = 7, de donde tienes la ecuación: a - b = 7,

q(2) = 29(2a + b) = 232, de donde tienes la ecuación: 58a + 29b = 232, dividimos en todos los términos de la ecuación por 29 y queda: 2a + b = 8.

Luego, queda para resolver el sistema de ecuaciones:

a - b = 7, de donde tenemos: a = b + 7 (*)

2a + b = 8,

reemplazamos en la segunda ecuación y queda:

3b + 14 = 8, de donde despejas y tienes: b = -2,

luego reemplazas en la ecuación señalads (*), resuelves y tienes: a = 5.

Luego, el polinomio queda:

q(x) = (2x^4 - 3)(5x - 2) = 10x^5 - 4x^4 - 15x + 6.

Espero haberte ayudado.

Espero haberte ayudado.

Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. Lo siento de corazón… Espero lo entiendasResponde esta pregunta...

Observa que puedes proponer la sustitución (cambio de incógnita): t = 3^x (*),

y observa que el denominador del segundo término de la izquierda puedes escribirlo: 3^(x+1) = 3^x * 3 = t*3 = 3t,

luego sustituyes y la ecuación queda:

t + 1 / 3t = 28/9, luego multiplicas por 3t en todos los términos de la ecuación y queda:

3t² + 1 = 84t / 9, luego multiplicas por 9 en todos los términos de la ecuación y queda:

27t² + 9 = 84t, luego haces pasaje de término, ordenas términos a la izquierda y queda:

27t² - 84t + 9 = 0, luego, como todos los coeficientes son múltiplos de 3, multiplicamos por ⅓ en todos los términos de la ecuación y queda:

9t² - 28t + 3 = 0, observa que tienes una ecuación polinómica cuadrática, aplicas la fórmula resolvente y tienes dos opciones:

a) t = 3, que al sustituir t por su expresión en función de x señalada (*) queda: 3^x = 3, lo que nos conduce a la solución: x = 1,

b) t = 1/9, que al sustituir t por su expresión en función de x señalada (*) queda: 3^x = 1/9 = 3^(-2), que nos conduce a la solución: x = -2.

Espero haberte ayudado.

En el ejercicio de la inecuación, puedes comenzar por distribuir el valor absoluto en la fracción y queda:

|2x - 1| / |3| ≥ 5, luego multiplicas por 3 en ambos miembros de la inecuación (observa que |3| = 3) y queda:

|2x - 1| ≥ 15, que nos conduce a dos opciones:

a) 2x - 1 ≥ 15, haces pasaje de término, resuelves y queda:

2x ≥ 16, multiplicas por 1/2 en ambos miembros y llegas a:

x ≥ 8

b) 2x - 1 ≤ -15, haces pasaje de término, resuelves y queda:

2x ≤ -14, multiplicas por 1/2 en ambos miembros y llegas a:

x ≤ - 7.

Por lo tanto, el conjunto solución expresado como intervalo queda: S = (-inf,-7] u [8,+inf).

Espero haberte ayudado.

En el ejercicio de las expresiones irracionales, observa que puedes expresar a las raíces con mínimo índice común, que en este caso es 12, y quedan:

Si tienes una potencia con exponente fraccionario, tienes que el denominador indica el ìndice de la raìz, y el numerador indica el exponente de la potencia:

x^(p/r) = (rV)(x^p).

En tus expresiones:

1) x^2 * 1/V(x^5) = expresamos el denominador del segundo factor como potencia con exponente 5/2:

= x^2 * 1/x^(5/2) = expresamos el divisor como factor con exponente opuesto, como indica el colega Enrique:

= x^2 * x^(- 5/2) = resolvemos el producto de potencias con bases iguales (recuerda que se suman los exponentes):

= x^(-1/2).

2) x^4 / (3V)(x^2) = expresamos el denominador como potencia con exponente 2/3:

= x^4 / x^(2/3) = expresamos el divisor como factor con exponente opuesto:

= x^4 * x^(-2/3) = resolvemos el producto de potencias con bases iguales:

= x^(10/3).

Espero haberte ayudado.

P.D: En el primer ejercicio a Don Antonio y a mí nos salen respuestas diferentes porque él consideró x^5 en el denominador de la fracción y yo tomé raíz décima de x^5...Así que tienes dos ejercicios para practicar   :)

Cuidado, Enrique:  1/( 3√x2  )   ≠  x-3/2 

Muchas gracias, me ha ayudado :)

raíznovena(x⁶)/x⁷ 

x³/raízcuarta(x³)

Explicación: cualquier número en el denominador está elevado a ^-1, por tanto 1/x²=x^-2. Por otra parte puedes comprobar con la calculadora que √2= 2^1/2, √2³=2^3/2, raizeésima(x^m)=x^m/2.

x^-7 x^6/9 =     x^-63/9 x^6/9   =  x^-57/9  = 1/x^57/9  =      1/ ⁹√x⁵⁷

Explicación:

Pasamos a común denominador los exponentes de x,

sumamos los exponentes al ser las bases iguales y estar multiplicandose,  

la potencia negativa se convierte en positiva si la pasamos del numerador al denominador

y por último lo convertimos en raíz

x³ x^-3/4  =          x^12/4 x^-3/4           =  x^9/4  =        ⁴√x⁹           

Explicación:

Pasamos a común denominador los exponentes de x,

sumamos los exponentes al ser las bases iguales y estar multiplicandose 

y por último lo convertimos en raíz            

Muchas gracias, me ha ayudado