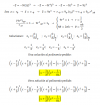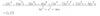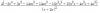-


Breaking Vlad
el 10/2/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-
Buenos días, necesito ayuda urgente, no soy capaz de resolver estos ejercicios, no encuentro por internet y tengo exámenes este martes, seguro que son los más sencillos😅. Por lo menos ver los métodos a seguir de uno de ellos, muchas gracias y un saludo
-
-
Hola buenas, no consigo realizar estas operaciones. ¿Podéis ayudarme?
a) Demuestra está igualdad
(senx cosx / cos²x - sen²x) = 1/2 (tg2x)
b) Resuelve está ecuación
sen2x + cos2x - 1 = cosx - 2sen²x

Sebastian Quintero
el 6/2/20La otra opción es partir del lado derecho recuerde que tan(u)=senu/ cosu aquí u=2x
Y luego usa las identidades del seno y coseno para el ángulo doble y listo.
Para la ecuación usamos la identidad del cos(2x) y hacemos lo posible para simplificar ...lo más posible es que muchas cosas se cancelen...luego deja todo igualado a cero y resuelve la ecuación resultante con alguna estrategia algebraica como la factorización
-
Buenas, me he encontrado con una operación con varias incógnitas que no soy capaz de resolver. Podrían intentarlo ustedes o decirme cómo se haría? Gracias.
Despues de factorizar no sé como continuar.
-
Alguien me ayuda resolviendo solo 1 o 2 para poder tener una idea para resolver luego por mi cuenta?,


Breaking Vlad
el 10/2/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)