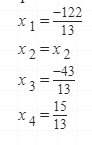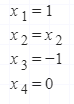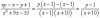-

 una consulta,si me dicen que ese vector es una de Las infinitas soluciones,interpreto que es SCI,quisiera saber si esta bien,no me quedo claro este ejercicio,desde ya gracias.ya lo ha resuelto antonius benedictus pero me quedo esa duda,preciso respuesta a la consulta,desde ya gracias.
una consulta,si me dicen que ese vector es una de Las infinitas soluciones,interpreto que es SCI,quisiera saber si esta bien,no me quedo claro este ejercicio,desde ya gracias.ya lo ha resuelto antonius benedictus pero me quedo esa duda,preciso respuesta a la consulta,desde ya gracias.
-
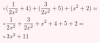 Esto está mal hecho no??, ese resultado solo podria darse si el x2 del demoninador, estuviera multiplicando al numerador
Esto está mal hecho no??, ese resultado solo podria darse si el x2 del demoninador, estuviera multiplicando al numerador

Soluciones Gratis
el 5/2/20Yo lo resolvi de la siguiente manera:multiplique a todo por 2x^2,para eliminarme el 2x^2 del denominador (pero hay que dividir el resultado obtenido por 2x^2)ya que manipule la operacion,el resultado seria x^2+(2/x^2)+11.para verificar si esta bien realizado me cree una funcion f (1). Reemplazando 1 en la incognita verifico si dan el mismo resultado,saludos.
-
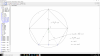
Hola a todos. Por favor necesito ayuda con este ejercicio, es más como dar una argumentación de por qué pasa eso, solo que no sé muy bien la razón, yo sé que se corre 3 unidades pues que en el denominador está x-3 pero no me parece un argumento valido, alguien por favor me puede explicar la razón.Muchas gracias