-
-


Breaking Vlad
el 4/2/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-


Breaking Vlad
el 4/2/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-
cúal el fue el punto de partida de newton y leibniz al cálculo?


Breaking Vlad
el 4/2/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-


Breaking Vlad
el 4/2/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-
¿Cómo se resolvería este problema? Gracias.
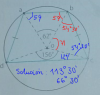
Calcula el lado de un pentágono regular inscrito en una circunferencia de radio 6m.

Antonio Silvio Palmitano
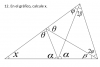
el 4/2/20Observa que si trazas todos los radios correspondientes a los vértices del pentágono regular, entonces tienes que esta figura queda dividida en cinco triángulos isóceles, con sus lados iguales con la medida del radio de la circunferencia, y con un ángulo cuya medida es: θ = 360°/5 = 72°, y cuyo tercer lado tiene la medida de uno de los lados del pentágono regular.
Luego, puedes aplicar el Teorema del Coseno, y queda la ecuación:
L2 = R2 + R2 - 2*R*R*cosθ, reduces los dos primeros términos, reduces factores semejantes en el tercer término, y queda:
L2 = 2*R2 - 2*R2*cosθ, extraes factores comunes, y queda:
L2 = 2*R2*(1 - cosθ), extraes raíz cuadrada positiva en ambos miembros, y queda:
L = √[2*R2*(1 - cosθ)], extraes el factor R, y queda:
L = √[2*(1 - cosθ)]*R,
que es la expresión de la longitud del lado del pentágono regular, en función del radio de la circunferencia en la cuál está inscrito, y del ángulo determinado por dos radios consecutivos.
Luego, solo queda que reemplaces valores (θ = 72°, R = 6 m), y hagas el cálculo.
Espero haberte ayudado.
-
Según Leibniz cúal fue el punto de partida del cálculo?


Breaking Vlad
el 4/2/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)