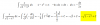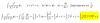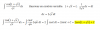-
Hola a todos. Alguien me puede orientar como hacer la siguiente demostración, la verdad por mas que leo no encuentro la forma de hacer esta demostración.
Demostrar que un sistema autónomo a11 + a22 = 1 no tiene soluciones periódicas.


Breaking Vlad
el 3/2/20Hola! Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-


Antonio Silvio Palmitano
el 31/1/20Vamos con una orientación.
Tienes la condición que cumplen los valores de la función h:
|h(x)| ≤ x2 - 1, despliegas esta inecuación según las propiedades de la función valor absoluto que has visto en clase, y queda:
-(x2 - 1) ≤ h(x) ≤ x2 - 1;
luego, tomas límites para x tendiendo a -1 en los tres miembros de esta inecuación doble (te dejo la tarea de plantearlos), resuelves el primero y el tercer miembro, y queda:
0 ≤ Lím(x→-1) h(x) ≤ 0,
por lo que puedes concluir, de acuerdo con el Teorema de Acotación:
Lím(x→-1) h(x) = 0.
Espero haberte ayudado.
-