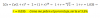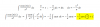-
Hola. Me pueden explicar este problema de interés simple. Lo resolví pero no me da el resultado, por favor.
El 7 de junio Marisela consigue un crédito por $45,000 para remodelar su sala de belleza, con cargos del 16.56% simple anual. Realiza un abono el 15 de agosto y otro por $15,750 el 20 de diciembre. ¿Por qué cantidad es el primer abono si el 15 de enero debe todavía $13,000?
a) $19,352.48 b) $18,973.21 c) $20,005.42 d) $19,038.26 e) Otra

Breaking Vlad
el 27/1/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-
-
-
Hola, un ejercicio de probabilidad:
1. Paula va a una tienda 2 veces por semana. Roberto trabaja en esta tienda 4 días por semana. Si el viernes es el único día que no van a la tienda ninguno de los dos,¿Cuál és la probabilidad de que coincidan dos días? (La tienda está cerrada el domingo)


Jose Ramos
el 26/1/20Casos posibles: Combinaciones (5,4) . Combinaciones (5,2) = 5 . 10 = 50
Casos favorables: Combinaciones (5, 4). Combinaciones (4,2) = 5. 6 = 30
Probabilidad de que coincidan dos días es 30/ 50 = 3 / 5 = 0,6
Trataré de explicarlo: Roberto va de los 5 días (L, M, Mi, J, S), 4 entonces las posibles combinaciones de días que tiene son LMMiJ, LMMiS,LMiJS, LMJS y MMiJS que son 5. En total Combinaciones de 5 tomados de 4 en 4. Por cada cuaterna de días que asista Roberto, Paula va dos días (LM, LMi,..., JS) En Total Combinaciones de 5 tomadas de 2 en 2 que son 10. Por tanto las posibilidades de asistencia combinada de ambos es 5. 10 = 50.
Ahora vamos con los casos favorables. Imaginemos que Roberto va los días LMJS Para coincidir dos días, Paula tiene que ir LM, LJ, LS, MJ, MS, JS. Fíjate que combinamos solo 4 días, descartamos el Miércoles pues Roberto no va ese día.
Por cada cuaterna que asiste Roberto, Paula puede asistir Combinaciones de 4 (retiro el día que no va Roberto) tomadas de 2 en 2 que son 6. Como Roberto tiene 5 cuaternas para asistir, el total de casos favorables es 5. 6 = 30.