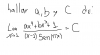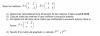-


Antonio Silvio Palmitano
el 4/12/16Comencemos por separar en dos factores el argumento del límite: uno racional y otro trigonométrico, y estudiemos el factor racional.
(ax4 + bx3+ 1)/(x - 1) (1)
Luego, en el numerador del primer factor, busquemos los valores de los coeficientes a y b para que 1 sea raíz doble del polinomio, y para ello empleamos dos veces la Regla de Ruffini y queda:
a b 0 0 1
1 a (a+b) (a+b) (a+b)
a (a+b) (a+b) (a+b) 1+(a+b)=0, de donde tenemos la ecuación: a + b = -1 (2)
1 a (2a+b) (3a+2b)
a (2a+b) (3a+2b) 4a+3b=0 (3);
luego resolvemos el sistema formado por las ecuaciones señaladas (2) (3), y su solución es: a = 3, b = - 4;
luego, el factor racional señalado (1) queda:
(ax4 + bx3+ 1)/(x - 1) = (3x4 - 4x3+ 1)/(x - 1) = factorizamos = (x - 1)2(3x2 + 2x + 1)/(x-1) = simplificamos = (x - 1)(3x2 + 2x + 1) (4).
Luego, tenemos para la expresión del argumento del límite:
( (ax4 + bx3 + 1)/(x - 1) ) * ( 1 / sen(πx) ) = sustituimos la expresión señalada (4):
= (x - 1)(3x2 + 2x + 1) * ( 1 / sen(πx) ) = ordenamos y asociamos factores:
= (3x2 + 2x + 1) * ( (x - 1) / sen(πx) ) (5), luego pasamos a estudiar el límite para el segundo factor (observa que el primero tiende a 6):
Lím(x->1) (x - 1) / sen(πx) =
hacemos la sustitución (cambio de variable): w = x - 1, de donde tenemos: w + 1 = x, y observa que w tiende a cero cuando x tiende a uno, sustituimos y queda:
= Lím(w->0) w /sen( π(w+1) ) = Lím(w->0) w /sen( πw+π ) = aplicamos identidad trigonométrica:
= Lím(w->0) w /(- sen(πw) ) = multiplicamos y dividimos por π:
= Lím(w->0) πw / π(- sen(πw) ) = extraemos factores constantes del denominador:
= ( 1/(-π) ) Lím(w->0) πw / sen(πw) = resolvemos (observa que tenemos un límite trascendente que seguramente has visto en clase):
= ( 1/(-π) ) * 1 = -1/π (6).
Luego, tenemos a partir de la expresión señalada (5) que el límite queda:
Lím(x->1) (3x2 + 2x + 1) * ( (x - 1) / sen(πx) ) = aplicamos la propiedad del límite de un producto:
= Lím(x->1) (3x2 + 2x + 1) * Lím(x->1) ( (x - 1) / sen(πx) ) =
resolvemos el primer factor, y reemplazamos el valor señalado (6) en el segundo factor::
= 6*(-1/π) = -6/π = C.
Espero haberte ayudado.
-
hola buenas quisiera saber si me podrian ayudar con este limite es por lhopital no se que hacer despues de ahi



David
el 5/12/16Lo que hiciste es perfecto! Ahora te toca aplicar LHOPITAL, derivando al numerador y denominador por separado...
La derivada de 1/x es -1/x²..
La derivada de (1+1/x)^x se hace por DERIVACION LOGARITMICA... Derivacion logaritmica¿Lo intentas y nos cuentas?
P.D. Determinar que el limite cuando x tiende a infinito de (1+1/x)^x es igual a "e" no requiere de demostración en tu curso y puedes decirlo inicialmente... -


Antonio Silvio Palmitano
el 4/12/16Vamos con una orientación: sabemos que el polinomio es de grado 3 y que su coeficiente principal es 2,
y que z1 = 2+i es una de sus raíces, por lo que planteamos:
P(x) = 2( x -(2+i) )(x2 + px + q) = 2(x - 2 - i)(x2 + px + q), con p y q a determinar.
Luego, planteamos:
P(1+2i) = 2(1 + 2i - 2 - i)( (1+2i)2 + p(1+2i) + q ) = 2(-1 + i)( (1+2i)2 + p(1+2i) + q ) (1),
luego, tenemos la última ecuación del enunciado:
P(1+2i) = 10(10 - 2i), sustituyes la expresión señalada (1) y queda la ecuación:
2(-1 + i)( (1+2i)2 + p(1+2i) + q ) = 10(10 - 2i), haces pasajes de factores constantes como divisores, simplificamos y queda:
(1+2i)2 + p(1+2i) + q = 5(10 - 2i)/(-1 + i), multiplicas en el segundo miembro por (-1 - i)/(-1 - i), resuelves y queda:
(1+2i)2 + p(1+2i) + q = 5(-12 - 8i)/2, resolvemos el segundo miembro y queda:
(1+2i)2 + p(1+2i) + q = - 30 - 20i, desarrollamos términos en el primer miembro y queda:
1 + 4i - 4 + p + 2pi + q = - 30 - 20i,
reducimos y agrupamos términos reales e imaginarios (suponemos que p y q son números reales) en el primer miembro y queda:
(- 3 + p + q) + (4 + 2p)i = - 30 - 20i, luego, por igualdad entre números complejos, tenemos el sistema de ecuaciones:
- 3 + p + q = -30
4 + 2p = - 20, de donde despejamos y queda: p = -12,
luego reemplazamos en la primera ecuación y queda. q = -15.
Por lo tanto, la expresión del polinomio queda:
P(x) = 2(x - 2 - i)(x2 - 12x -15).
Espero haberte ayudado.
-
considerando las matrices siguientes A= 1 -2 B= 2 -1 C= 3 -12
0 1 1 1 0 5
calcula X para que se cumpla A² . X -B =C ayuda resolviendo este ejercicio :(
-
Por favor ayudadme con este ejercicio, mañana tengo examen, muchas gracias de antemano :D.



David
el 5/12/16SUSTITUYE X POR 1 en el primer trozo e iguala a 1... Obtendrás una ecuación..
Intenta hacer el limite por la izquierda y por la derecha e igualalos (para que se a continua)....
Tendrás otra ecuacion. Resuelve el sistema...
Te sugiero los vídeos de "discontinuidad en una funcion a trozos" -
Hola, haciendo los ejercicios resueltos de matrices me he encontrado con que el ejercicio 3 está mal. El enunciado pone tenemos que hallar la x para que A2 - xA + yI = 0 y en la solución pone: Calculamos A2 - xA - yI e igualamos a 0 por lo que todo el ejercicio está mal.
-
 Me gustaría saber por qué al factorizar esta fracción se cambia de signo la primera x del numerador y todo el denominador, gracias!!
Me gustaría saber por qué al factorizar esta fracción se cambia de signo la primera x del numerador y todo el denominador, gracias!!