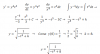Hola! Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas

Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)

¡Muchas gracias de verdad!

En estos ejercicios, cuando consideras un rectángulo o un polígono en general, se toman los vértices consecutivos (en este caso incluso te lo dice el enunciado). Consecutivos quiere decir que tienen que ir ordenados, bien en el sentido de las agujas del reloj o en sentido contrario. En tu dibujo los has colocado no consecutivos y eso es lo que te induce a error.  Mira el dibujo y lo entenderás:

Muchas gracias! Lo he entendido perfectamente. Entonces para evitar errores mejor lo aplico a todos los ejercicios que me pidan este tipo de figuras no?

Para despejar t hay que aplicar logaritmos como puedes ver en la siguiente solución:

Vale muchas gracias

Para la función f(x):   Dominio (-∞, +∞)   Recorrido (-∞,0]. Tendencias más significativas:  lim (x-> -2) f(x) = 0;   lim (x->2) f(x) = 0

Para la función h(x):  Dominio (-∞,0)∪(2,+∞)   Recorrido (0, +∞). Tendencias más significativas:  lim (x->0-) h(x) = +∞;  lim (x->2+) h(x) = +∞; lim (x->+∞) h(x) = 0; lim (x->-∞) h(x) = 0.  Asíntotas  x = 0  por la izquierda,  x = 2 por la derecha,   e y = 0.

Muchas gracias, las tendencias son lo que más me cuesta así que me ayudaste mucho.

¡Muchas gracias!

A la primera integral añádele la constante.

La derivada está mal:

La constante C? Esta puesta

Me refiero a la fórmula general del principio.