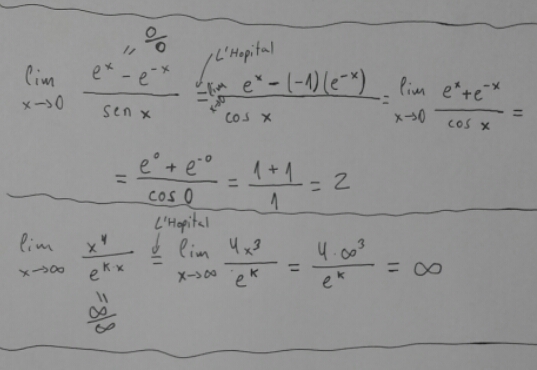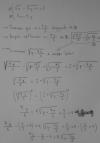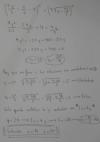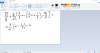
-
Usuario eliminado
el 28/11/16
Resulta que haciendo un problema de química de equilibrio al final me da la siguiente ecuación de la que tengo que despejar x:
5 84·10^-3 = [(0 5+2x)/20]^2 / [4 14-x/20]Vista así, cuesta un poco imaginarle pero básicamente igualan 5 84·10^-3 a [(0 5+2x)/20]^2 partido de [4 14-x/20]
Al final, por arte de magia sin hacer ningún paso intermedio despejan x= 0 092 moles.
Si me dierais al menor alguna pista, lo agradecería, entiendo que de ahí sale una ecuación de segundo grado de la que igualmente, me da dos valores y no sé cuál coger (aunque igualmente ninguno me da 0 092 jaja)
MUCHAS GRACIAS!!!!!Aquí dejo una foto. Realmente es un problema de química pero la duda es matemática
(IGNORAD EL 2 QUE VIENE DETRÁS DE MOLES, ES UN ERROR)
Antonio Silvio Palmitano
el 28/11/16Puedes comenzar con pasaje de divisor como factor, y queda la ecuación:
5,84*10-3 * (4,14 - x)/20 = ( (0,5 + 2x)/20 )2, resolvemos factores en el primer miembro, y desarrollamos en el segundo miembro y queda:
2,92*10-4 * (4,14 - x) = (0,25 + 2x + 4x2)/400, hacemos pasaje de divisor como factor, resolvemos factores en el primer miembro y queda:
11,68*10-2 * (4,14 - x) = 0,25 + 2x + 4x2, distribuimos en el primer miembro y queda:
48,3552*10-2 - 11,68 *10-2 x = 0,25 + 2x + 4x2, hacemos pasajes de términos, reducimos, ordenamos y queda:
- 4x2 - 2,1168x + 0,233552 = 0, dividimos en todos los términos de la ecuación por -4 y queda:
x2 + 0,5292x - 0,058388 = 0, luego aplicamos la fórmula resolvente para ecuaciones polinómicas cuadráticas y las soluciones son:
a) x ≅ 0,093731,
b) x ≅ - 0,622931 (que no tiene sentido para este problema).
Espero haberte ayudado.
-
Marian
el 28/11/16 -
Jesús Martínez Verdejo
el 28/11/16 -
Antonella Correa
el 28/11/16Hola! Necesito ayuda con un ejercicio sobre limites aplicando l´hopital, acá está el enunciado
Antonio Silvio Palmitano
el 28/11/16Vamos con el segundo ejercicio. Tienes:
Lím(x->inf) x4/ekx = observa que es indeterminado (el numerador y el denominador tienden ambos a infinito), aplicamos la Regla de L'Hôpital:
= Lím(x->inf) 4x3 / kekx = observa que continúa indeterminado, aplicamos nuevamente la Regla de L'Hôpital y queda:
= Lím(x->inf) 12x2 / k2ekx = observa que continúa indeterminado, aplicamos nuevamente la Regla de L'Hôpital y queda:
= Lím(x->inf) 24x / k3ekx = observa que continúa indeterminado, aplicamos nuevamente la Regla de L'Hôpital y queda:
= Lím(x->inf) 24 / k4ekx= 0 (observa que el numerador es constante, y que el denominador tiende a infinito).
Espero haberte ayudado.
-
Francesc Llobera Bennasar
el 28/11/16- Alguien me puede ayudar con este sistema de ecuaciones no lineales, lo he probado de todos modos pero no me sale
- {√x - √y-x = 2
- {5x=4y
Antonius Benedictus
el 28/11/16
Ángel
el 28/11/16 -
Elena Abad
el 28/11/16En las sumas y restas de fracciones algebraicas, solo se saca mcm en el denominador?
Ángel
el 28/11/16Sí Elena,
para tenerlo más claro mira el ejercicio resuelto que le he mandado a ALOFRE en el mensaje de más abajo
Observa que si tenemos 3/4 y el mcm=24 en el denominador, para sacar el numerador tendremos que dividir 24 entre 4, y eso multiplicado por 3: que resultaría 18
Por lo tanto 3/4=18/24, son fracciones equivalentes
-
ALOFRE
el 28/11/16 -
Diego
el 28/11/16Hola tengo un problema con un ejercicio de distribución normal que es el siguiente:
Las notas de un curso se distribuyen según una N(5, 1). ¿A partir de qué nota se concederá Matrícula de Honor si se pretende que el 2'5% de los alumnos obtengan tal calificación?
¿Tengo que tipificar para pasar a una N(0, 1)? ¿Y en ese caso como lo hago con los datos que tengo?
Gracias de antemano.
-
carmen
el 28/11/16no se seguir la serie
1
11
21
1211
111221
César
el 28/11/16La secuencia de números enteros "look-and-say" fue introducida y analizada por el matemático John Conway, conocido por el famoso Juego de la vida. Esta secuencia tiene la forma: 1, 11, 21, 1211, 111221, 312211, ...
Su construcción es sencilla, cada término describe al anterior: 1 contiene "un uno", o sea, 11; 11 contiene "dos unos", o sea, 21; 21 contiene "un dos y un uno", o sea, 1211; 1211 contiene "un uno, un dos y dos unos", o sea, 111221; 111221 contiene "tres unos, dos doses y un uno", o sea, 312211. -
carmen
el 28/11/16Jaime e Irene, dos amigos de la infancia, se encuentran en el centro de Granada paseando y llevaban años sin verse. Ambos se alegran mucho, se saludan y dialogan: - Jaime: ¿Tienes hijos? - Irene: Sí, tengo tres. - Jaime: ¿Qué edad tienen? - Irene: El producto de sus edades es 36 y la suma de las mismas es igual al número del edificio de enfrente.
Jaime se queda pensando por un tiempo, y después, mientras mira en el número de la casa de enfrente dijo:
- Jaime: Necesito saber más. - Irene: Es cierto, mi hija mayor se llama Irene, como yo.
Con estos nuevos datos Jaime pudo calcular la edad de los tres hijos de Irene. Resuelve tú también el enigma calculando sus edades
nopuedo solucionarlo alguien me podria ayudar muchas gracias
César
el 28/11/16Jaime sabe la suma de las edades, pues ve el número del portal.
Factorizando los posibles porductos y su suma tenemos
. . . . . . . . . . . . . . suma
{1, 1, 36} ---------- 38
{1, 2, 18} ---------- 21
{1, 3,12} ----------- 16
{1, 4, 9} -------------14
{1, 6, 6} -------------13
{2, 2, 9} -------------13
{2, 3, 6} -------------11
{3, 3, 4} -------------10Del dato facilitado por Irene al final , sabemos que solo hay una hermana mayor, asi que las ternas posibles son
{1, 1, 36} ---------- 38
{1, 2, 18} ---------- 21
{1, 3,12} ----------- 16
{1, 4, 9} -------------14
{2, 2, 9} -------------13
{2, 3, 6} -------------11
{3, 3, 4} -------------10Parece que todas cumplen el enunciado, una hija mayor y dos mas pequeñas incluidas gemelas.
No creo que pueda afirmarse mas con ese enunciado, pues el edificio de enfrente puede ser 10,11,13,14,16,21,38.
