-
alguien que me ayude con este problema de integral por favor llevo 3 dias intentando resolverlo y no puedo :(



Antonio Silvio Palmitano
el 28/11/16Haz un gráfico, y verás que el sólido tiene base triangular en el plano xy, con vértices: (0,0), (7,0), (0,1), y que puedes plantear para esta región, que los lados del triángulo base están sobre las rectas cuyas ecuaciones son: x = 0, y = 0, y = (-1/7)x + 1.
Luego, la región queda descrita con el sistema de desigualdades dobles:
0 ≤ y ≤ (-1/7)x + 1
0 ≤ x ≤ 7.
Luego, para calcular el volumen del sólido, podemos plantear, con la ecuación explícita del plano: z = 7 - x - 7y:
V = ∫∫ (7 - x - 7y) dy dx,
y puedes continuar la tarea (observa que los límites de integración están expresados en las desigualdades dobles).
Espero haberte ayudado.
-


David
el 29/11/16Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
No se si alguien me podrá ayudar con este problema o estará apto; pero el problema es el siguiente: Un agricultor desea poner una cerca alrededor de un campo rectángular si el agricultor puede comprar solo 100 yardas de cerca. a) expresa el largo en función del ancho. b) Qué dimensiones darán el máximo del área rectángular?

Tomoharu
el 28/11/16100 yardas=91.44 metros de cerca.
a) Es un campo rectangular asi que Perimetro(La cerca) = 2A+2L o sea 100 yardas = 2Ancho+2Largo entonces despejando el largo:
(100/2)=A+L----> L=50-A
b) Tenes que encontrar el maximo de area,osea 2 numero distintos que al multiplicarse den la maxima area posible,eso numeros son L y A. Asigna valores a A y en tu funcion creada en A multiplica ese valor por la L resultante para ver que combinacion da la mayor area.
No comprendi muy bien lo que pedia pero espero haberte sido de ayuda
-
Voy a entrar a estudiar ingeniería ambiental ¿me pueden decir que tengo que fortalecer (algún tema o materia) para no quedar frustrado en la universidad ?

Ángel
el 30/11/16De mayor a menor importancia para ingeniería ambiental:
Química
Biología
Matemáticas (derivadas, integrales, probabilidad y estadística)
Física
Aunque química sea la más importante, no olvides que si fallas mucho en alguna de estas 4 asignaturas te costará más de lo normal...así que a "fortalecer" desde ya (los 3 foros de unicoos son un muy buen apoyo)
-
Holas, por favor ayudadme con este ejercicio:
Determine las dimensiones del cilindro de mayor volumen que pueda inscribirse en una esfera de 6m de radio.
Muchas gracias :)
-
Hola!!! hay un ejercicio que no lo estoy podiendo hacer hace mil y no me sale, y necesito algo de ayuda. y es que tengo que hallar el valor que debe tener "m" para que el resto de la división del polinomio
2X3 - mX2 +3 por el polinomio x+1 sea -1. Una vez que obtegnido el valor de "m" tengo que resolver la división aplicando la regla de Ruffini. ¿no entindo como tengo que resolver el ejercicio?
Gabriel
el 28/11/16Te ayudamos.
Hay una norma que dice que si al Dividendo D(x)=2x3-mx2+3, sustituyes la "x" por el valor de la raíz del monomio que te dan como Divisor, en este caso x+1, que para transformarlo a raíz lo igualamos a cero, x+1=0, por lo que x=-1, el resultado que te da es el resto. Es decir Dividendo sustituyendo la x del Divisor, y el resultado es el resto.
D(-1)=2(-1)3-m(-1)2+3=-1
-2-m+3=-1
m=2
Nos queda D(x)=2x3-2x2+3
Y ahora aplicar Rufini.
Division de polinomios Ruffini
-
No pido la resolución de todos, simplemente una manera de cómo encarar esos polinomios :-)
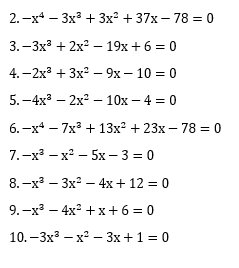

Mario
el 28/11/16Hola Peter, se me curre para resolverlos por "ruffini", probando raices...... o sino creo que en la pag, hay videos de integrales de ese tipo, algo asi como formula de cardano o cordano...
factor comun es un poco complicado porque tenes terminos independientes y ahi si no se como podes hacerlo. O sino quizas encontrar posibles raices y reducirlo aun mas, pero esto esta relaccionado con el primer metodo q te menciono. En particular en algunas ocaciones uso dicho metodo y me ayuda bastante.
espero haberte ayudado un poquito
saludos. :)
-


Antonio Silvio Palmitano
el 28/11/16Puedes comenzar por multiplicar y dividir la expresión por la expresión "conjugada" del numerador, lo haces y queda (indicamos con N al numerador y con D al denominador):
N = ( c√(c2/g2 + 1/4) - c2/g )( c√(c2/g2 + 1/4) + c2/g ) = desarrollas y simplificas = c2(c2/g2 + 1/4) - c4/g2 = c2/4;
D = c√(c2/g2 + 1/4) + c2/g = extraemos factor común c2 en el argumento de la raíz = c√( c2(1/g2 + 1 / 4c2) ) + c2/g =
distribuimos la raíz y resolvemos en el primer término
= c2 √( 1/g2 + 1 / 4c2) + c2/g = extraemos factor común = c2( √( 1/g2 + 1 / 4c2) + 1/g ).
Luego, observa que al plantear el cociente, podemos simplificar c2, y la expresión queda:
h(c) = N/D = (1/4) / ( √( 1/g2 + 1 / 4c2) + 1/g ), luego pasamos al límite (observa que el denominador tiende a 2/g):
Lím(c->+inf) h(c) = Lím(c->+inf) 1/4 / ( √( 1/g2 + 1 / 4c2) + 1/g ) = (1/4) / (2/g) = g/8.
Espero haberte ayudado.
























