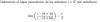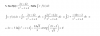Observa que aplicamos identidades trigonométricas y queda:

cotg²x = cos²x / sen²x = (1 - sen²x) / sen²x = 1/sen²x - sen²x/sen²x = 1/sen²x -  1.

Luego, pasamos a la integral:

I = ∫ cotg²x dx = ∫ (1/sen²x -  1)dx = ∫ (1/sen²x)dx - ∫ 1dx = - cotgx - x + C.

Espero haberte ayudado.

Muchas gracias!

Por fracciones parciales dayra:-)

∫ dx/(x²-x+1)²= (Ax + B) / x²-x+1  + (Cx +D) / (x²-x+1)²

Observa que aplicamos propiedad del logaritmo de una división, luego del logaritmo de una potencia, y podemos escribir la expresión de la función en la forma:

f(x) = ln(1) - ln(x²) = 0 - 2lnx = -2lnx, luego derivamos:

f ' (x) = -2(1/x) = -2/x.

Espero haberte ayudado.

Observa que el numerador en la expresión fraccionaria del primer trozo puede escribirse:

x² - (a+3)x + 3a = (x-a)(x-3), y luego la expresión simplificada queda:

(x-a)(x-3)/(x-3) = x -a.

Luego, la expresión de la función a trozos queda:

f(x) =

x - a         si x ≠ 3

1              si x = 3

observa que para tener continuidad en x = 3, el valor de a debe ser 2.

Luego, observa que para el primer trozo, la función derivada toma el valor constante 1, por lo que tenemos que el valor es el mismo para x = 3:

f ' (x) =

1             si x ≠ 3

1             si x = 3

por lo tanto, tenemos que f ' (x) = 1, para todo valor real x y, en particular, tenemos:

f ' (3) = 1.

Espero haberte ayudado.

Hola. Una apreciación Antonio.

Si para calcular la derivabilidad en x=3, tenemos que calcular la derivada de la función. por lo que la derivada de f=1, sería f'x=0, por lo que f'(3)=0, ¿no? :|

Debes tener en cuenta la definición de función derivada en un punto, en este caso 3, y observa que la función toma el valor 1 sólamente para 3 (es la definición de la función para ese único punto), y para el resto toma los valores x-2. Queda:

f(x) = 

x - 2      si x ≠ 3

1           si x = 3.

Luego, pasamos a la definición de derivada, para calcularla para x = 3:

Planteamos el numerador del cociente incremental:

f(3+h) - f(3) = observa que el primer término corresponde al primer trozo, y el segundo término corresponde al segundo trozo:

= ( (3+h) - 2) - 1 = resolvemos agrupamientos:

= 3 + h - 2 - 1 = h.

Luego pasamos al límite del cociente incremental:

f ' (3) = Lím(h->0) ( f(3+h) - f(3) )/h = sustituimos en el numerador:

= Lím(h->0) h/h = Lím(h->0) 1 = 1.

Espero haberte ayudado.

Se separa en 2 integrales debido a que en el integrando se encuentran polinomios del mismo grado, por tanto se procede

a realizar el cociente de polinomios.

Tenías que haberme dicho que no sabes hacer integrales.

La F está mal (revisa el área del triángulo)

1) Observa que para a = 1, la segunda ecuación queda:

(1-1)x = 1, resuelves el coeficiente y queda: 0x = 1, resuelves el primer miembro y queda: 0 = 1, que es una identidad absurda, y el sistema resulta incompatible.

2) Si a = 2, reemplazas y el sistema de ecuaciones queda:

x + y + 2z = 0

x               = 1

x + 3y      = 2

           0z = 0, que conduce a la identidad verdadera 0 = 0,

luego reemplazamos en la primera y la tercera ecuación, hacemos pasajes de términos en ambas ecuaciones y el sistema queda:

  y + 2z = -1

3y         =  1, de donde despejamos y tenemos: y = 1/3,

luego reemplazamos en la primera ecuación, hacemos pasaje de término y queda:

2z = - 4/3, de donde despejamos y tenemos: z = - 2/3.

Luego, el sistema resulta compatible determinado, y su solución es: x = 1, y = 1/3, z = - 2/3.

Espero haberte ayudado.

Distribucion binomial
Distribución normal

etc, etc, etc.. #nosvemosenclase

okay muchas gracias