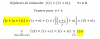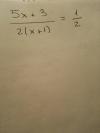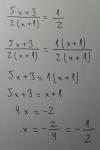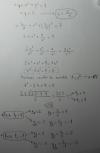-
Alberto
el 21/11/16Hola necesito que alguien me ayude con una demostración.
Necesito demostrar que si una función es periódica f(x)=f(x+nL) ∀ x ∈ ℛ, ∀ n ∈ ℕ donde L es el periodo de f.
Lo estoy intentando por inducción pero no se como lo tengo que hacer, se supone que es 1º x=1; 2º suponemos que para x es cierto; 3º demostramos x+1
1º hago x=1 --> f(1)=f(1+nL) , con eso demuestro que para x=1 se cumple??
2º supongo que f(x)=f(x+nl) es cierto
3º hago f(x+1) -> f(x+1)=f(x+1+nL) como sigo?
-
The punk
el 21/11/16
Hola amigos de unicoos necesito ayuda con un ejercicio de geometría, yo para resolverlo despejo una variable de una ecuación y la reemplazo en la otra quiero saber si es correcto lo hago, les dejo una foto del enunciado
David
el 21/11/16
Antonio Silvio Palmitano
el 22/11/16Van orientaciones.
a) La segunda ecuación corresponde a un plano paralelo al plano coordenado XZ, despeja y, y luego sustituye en la primera ecuación.
b) La segunda ecuación corresponde a un plano paralelo al plano coordenado XY, despeja x, y luego sustituye en la primera ecuación.
c) La segunda ecuación corresponde a un plano que corta a los tres ejes coordenados, despeja y, y luego sustituye en la primera ecuación.
d) La segunda ecuación corresponde a un plano que corta a los tres ejes coordenados, despeja z, y luego sustituye en la primera ecuación.
Observa que en los últimos dos ejercicios, hemos propuesto despejar la variable de la segunda ecuación que figura sin exponente en la primera, solo para facilitar el trabajo.
Observa que en los cuatro ejercicios, una vez hechos los despejes y sustituciones, quedan intersecciones entre un plano y una superficie cilíndrica: a) hiperbólica, b) elíptica, c) hiperbólica, d) elíptica.
Recuerda que en R3 siempre representamos a las curvas como intersecciones entre superficies, cuando empleamos coordenadas cartesianas.
Espero haberte ayudado.
-
Sau
el 21/11/16 -
Shalinza Dun Modr
el 21/11/16Hola! me echáis un cable? Gracias de antemano!
-
andres
el 21/11/16Buenas podrían ayudarme con el apartado a y b por favor? No consigo entender los sistemas de ecuaciones no lineales
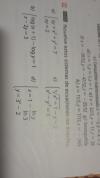
Antonio Silvio Palmitano
el 21/11/16Vamos con orientaciones.
a) A la primera ecuación le restamos la segunda, mantenemos la segunda ecuación, y el sistema queda:
x2 + y2 = 5
xy = 2, de aquí despejamos: y = 2/x (*), luego sustituimos en la primera ecuación y queda:
x2 + (2/x)2 = 5, distribuimos el exponente en el segundo término y queda:
x2 + 4/x2 = 5, multiplicamos en todos los términos por x2 y queda:
x4 + 4 = 5x2, hacemos hacemos pasaje de término y queda:
x4 - 5x2 + 4 = 0, luego, observa que es una ecuación polinómica bicuadrática, planteamos la sustitución w = x2 (**), sustituimos y queda:
w2 - 5w + 4 = 0, cuyas soluciones son:
1) w = 1,
2) w = 4
Luego queda para que sustituyas en la expresión señalada (**) para determinar los valores de x, y luego en la expresión señalada (*) para determinar los valores de y.
Observa que el sistema tiene cuatro soluciones.
b) Trabajamos la primera ecuación:
log(x + 1) - logy = 1, aplicamos la propiedad del logaritmo de una división:
log( (x + 1)/y ) = 1, luego componemos con la función inversa del logaritmo decimal en ambos miembros:
(x + 1)/y = 10, luego hacemos pasaje de divisor como factor y queda:
x + 1 = 10y, hacemos pasajes de términos y queda:
x - 10y = -1, luego, el sistema de ecuaciones queda:
x - 10y = - 1
x - 2y = 3
Observa que es un sistema de dos ecuaciones lineales con dos incógnitas, que seguramente podrás resolver con facilidad (su solución es: x = 4, y = 1/2).
Espero haberte ayudado.
-
Silvia Alonso Toledano
el 21/11/16Hola buenas tardes , no acabo de comprender muy bien este ejercicio , ¿ alguien me puede ayudar ? muchas gracias.
-
Sau
el 21/11/16 -
benson
el 21/11/16Obtén una aproximación para las siguientes raíces de las siguientes funciones con un error inferior al indicado.
1.Raíz aproximada de g(x)=2x-3x en (2,4) con error inferior a 0,3 2. h(x)= x - 3/x² en (1,4) con error inferior a 0,4
¿Podrían ayudarme no tengo ni idea de como resolver estas funciones?
David
el 21/11/16Tus ejercicios corresponden a Polinomio de Taylor, McLaurin, Resto...
Polinomio de Taylor con Resto de una funcion trigonometrica
No puedo ayudarte mucho mas, más allá de los vóideos que grabé como excepción de este tema. Espero lo entiendas. -
inmaculada
el 21/11/16alguien podria decirme cual es la continuidad y el dominio de e^1/x?
mil gracias ante todo <3
Antonio Silvio Palmitano
el 21/11/16Observa que la función resulta de la composición entre dos funciones cuyas expresiones son:
g(x) = ex, cuyo dominio es R
f(x) = 1/x. cuyo dominio es R - {0}.
Luego, tenemos la función compuesta:
(g o f)(x) = g( f(x) ) = g( 1/x ) = e1/x
cuyo dominio es R - {0}.
Recuerda que el dominio de la función compuesta debe estar incluido en el dominio de la primera función y, a lo sumo, puede coincidir con él, como ocurre en este caso.
Espero haberte ayudado.
-
Sau
el 21/11/16Hola buenas, me podrían ayudar con este ejercicio. Tengo algunos problemas para comprenderlo y necesito ayuda. Gracias.
David
el 21/11/16Por ejemplo, solo tienes que dividir 1 entre 6 y efectuar una resta para obtener el valor absoluto...
Error absoluto y relativo
A partir de ahí, el trabajo duro tiene que ser el tuyo. si nos envías una foto (más pequeña por favor) con lo que consigas por ti mismo, te echamos un cable ¿ok?
