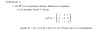-
Espero no molestarlos, solo que no domino muy bien estos temas, me ayudarian con este tambien.
Se los pido de mucho favor,
Una agencia de automóviles sabe por experiencia que su venta anual asciende a 100,000 unidades por año y los solicita a la armadora en lotes de tamaño x. Le cuesta a la agencia $1,000.00 la colocación de cada pedido y los costos de almacenaje por automóvil son de $200.00 al año. Con esta información calcula el tamaño óptimo de cada lote para minimizar la suma del costo del pedido y el de almacenaje.


David
el 21/11/16¿Has visto los vídeos de PROGRAMACION LINEAL? Programación lineal
Se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado, pero no olvidéis de adjuntarlo de forma LITERAL, para saber que os piden. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-


Antonius Benedictus
el 19/11/16Una matriz es hermítica o autoadjunta cuando es igual a su propia adjunta y es antihermítica cuando es igual a su traspuesta conjugada multiplicada por -1.
Sobre espacios vectoriales reales, las matrices hermíticas coinciden con las matrices simétricas y las antihermíticas con las antisimétricas. Estos operadores se pueden representar como una matriz diagonal (en una base ortonormal) de números reales. Este concepto se puede generalizar a un espacio de Hilbert de dimensión arbitraria.
-
Hola Buenas tardes, me podeis ayudar alguien, con el siguiente problema?
De ante mano, muchas gracias.
Una empresa productora de lámparas obtiene una utilidad de $5.00 por cada artículo vendido, pero tiene un gasto de A pesos a la semana por concepto de publicidad; considerando que su ecuación de demanda está dada por x = 2,000(1-e-0.001A); calcula el valor de A que optimice la utilidad del fabricante y determina su monto.
-
 Buenas tardes! Alguien sabrìa decirme que valor de "a" tendrìa que tomar para estimar el error? Gracias!
Buenas tardes! Alguien sabrìa decirme que valor de "a" tendrìa que tomar para estimar el error? Gracias!

Antonio Silvio Palmitano
el 18/11/16Observa que la expresión de la derivada de orden cuatro de la función puede escribirse:
fIV(x) = (4+x)ex
Luego, la expresión de Lagrange para el resto queda:
R3(x) = ( fIV(c)/4! )x4 = ( (4+c)ec/24)x4, con c comprendido entre 0 y x.
Luego, evaluamos para x = -0,1 y queda:
R3(-0,1) = ( fIV(c)/4! )(-0,1)4 = ( (4+c)ec/24 )(-0,1)4, con -0,1 ≤ c ≤ 0.
Luego pasamos a acotar el resto:
R3(-0,1) ≤ | R3(-0,1) | = | ( (4+c)ec/24 )(-0,1)4 | = ( (4 + c)ec/24 )(-0,1)4 ≤ observa que el valor se maximiza si acotamos c con cero:
≤ ( (4 + 0)e0/24 )(-0,1)4 = (4*1/24)(0,0001) = (1/6)(1/10000) = 1/60000.
Por lo que tenemos que el resto queda acotando: - 1/60000 ≤ R3(-0,1) ≤ 1/60000.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 18/11/16Se llama antilogaritmo a la función inversa del logaritmo.
Por ejemplo, la expresión de la función inversa del logaritmo en base 2, es:
antilog2(x) = 2x (también se la llama función exponencial en base 2).
Luego pasamos al ejercicio, trabajamos con el primer miembro para luego igualar:
comencemos por calcular: antilog23 = 23 = 8;
luego continuamos con (indicamos raíz cuarta como (4V)): antilog(4V)(2)8 = ( (4V)(2) )8 = simplificamos índice y exponente = 22 = 4;
luego concluimos con: antilogx4 = x4 = 16, luego expresamos a 16 como potencia con base 2:
x4 = 24, por último, comparamos bases y llegamos a:
x = 2.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 18/11/16Observa que tienes un sistema de tres ecuaciones con tres incógnitas, por lo que puedes plantear el determinante (D3) de la matriz del sistema (cuyos elementos son los coeficientes de las incógnitas), y pueden darse dos opciones:
a) D3 ≠ 0, y el sistema es compatible determinado, o b) D3 = 0 y el sistema es incompatible o compatible indeterminado.
Planteamos la matriz ampliada del sistema (remarcamos los elementos del determinante D3):
1 2 -a 3
2 (a-5) -1 (4a+2)
4 (a-1) -3 4
Luego, desarrollas el determinante y quedan seis términos en su expresión:
D3 = -3(a - 5) - 2a(a -1) - 8 + 4a(a - 5) + (a - 1) + 12, distribuimos y queda:
D3 = - 3a + 15 - 2a2 + 2a - 8 + 4a2 - 20a + a - 1 + 12, reducimos términos, ordenamos y queda:
D3 = 2a2 - 20a + 18, extraemos factor común y queda:
D3 = 2(a2 -10a + 9), factorizamos la expresión cuadrática y queda.
D3 = 2(a - 1)(a - 9).
Luego pasamos a analizar los casos:
a) Si a ≠ 1 y a ≠ 9, entonces tienes: D3 ≠ 0, y el sistema resulta compatible determinado.
b) Si a = 1 o a = 9, entonces tienes: D3 = 0, y el sistema puede resultar ser incompatible o compatible indeterminado y, para precisar, reemplazamos cada opción en la matriz:
b1) Para a = 1 la matriz queda:
1 2 -1 3
2 -4 -1 6
4 0 -3 4
A la fila 2 le restamos el doble de la fila 1, y a la fila 3 le restamos el cuádruple de la fila 1:
1 2 -1 3
0 -8 1 0
0 -8 1 -8
A la fila 3 le restamos la fila 2:
1 2 -1 3
0 -8 1 0
0 0 0 -8
Puedes observar que la última fila conduce a la identidad absurda: 0 = - 8, por lo que el sistema resulta ser incompatible.
b2) Para a = 9 la matriz queda:
9 18 -9 3
2 4 -1 38
4 8 -3 4
Multiplicamos a la fila 1 por 1/3 y queda:
3 6 -3 1
2 4 -1 38
4 8 -3 4
A la fila 1 le restamos la fila 2:
1 2 -2 -37
2 4 -1 38
4 8 -3 4
A la fila 2 le restamos el doble de la fila 1, y a la fila 3 le restamos el cuádruple de la fila 1:
1 2 -2 -370 0 3 112
0 0 5 152
A la fila 2 la multiplicamos por 1/3, y a la fila 3 la multiplicamos por 1/5:
1 2 -2 -37
0 0 1 112/3
0 0 1 152/5
A la fila 3 le restamos la fila 2, y queda:
1 2 -2 -37
0 0 1 112/3
0 0 0 -104/15
Puedes observar que la última fila conduce a la identidad absurda: 0 = - 104/15, por lo que el sistema resulta ser incompatible.
Espero haberte ayudado.
-
¿Alguien tan amable de ayudarme a resolver este horror? sen(2x)·cosx=6·sen^3x
Gracias :((


Antonio Silvio Palmitano
el 18/11/16Debes tener en cuenta la identidad trigonométrica: sen(2x) = 2senx*cosx, sustituimos y la ecuación queda:
2senx*cosx*cosx = 6sen3x, dividimos por 2 en ambos miembros, hacemos pasaje de término y queda:
senx*cosx*cosx - 3sen3x = 0, extraemos factor común, reducimos factores y queda:
senx(cos2x - 3sen2x) = 0, luego, por anulación de un producto, tenemos dos opciones:
a) senx = 0, que corresponde a: x = 0, 180°, 360°,...., en general: x = 180°*k, con k ∈ Z;
b) cos2x - 3sen2x = 0, hacemos pasaje de término y queda:
- 3sen2x = - cos2x, hacemos pasajes de factores como divisores y queda:
sen2x/cos2x = 1/3 = 3/9, aplicamos la identidad trigonométrica de la tangente y queda:
tan2x = 3/9, luego hacemos pasaje de potencia como raíz y tenemos dos opciones:
b1) tanx = √(3)/3, que corresponde a los ángulos:
x = 30° (en el primer cuadrante), en general: x = 30° + 360°*k, con k ∈ Z,
x = 210° (en el tercer cuadrante), en general: x = 210° + 360°*k, con k ∈ Z.
b2) tanx = - √(3)/3, que corresponde a los ángulos:
x = 150° (en el segundo cuadrante), en general: x = 150° + 360°*k, con k ∈ Z,
x = 330° (en el cuarto cuadrante), en general: x = 330° + 360°*k, con k ∈ Z.
Espero haberte ayudado.
-
Me ayudan con este ejercicio de probabilidad?
Tres máquinas A B y C producen: A (60 piezas no defectuosas y 3 defectuosas), B (90 no defectuosas y 5 defectuosas) y C (230 no defectuosas y 12 defectuosas)
Hallar la probabilidad: a) de que una pieza salga de C y sea defectuosa.
b) de que una pieza de la maquina C sea no defectuosa
Gracias
-
Buenos días me gustaría si podéis que me echarais una mano con este ejercicio, muchas gracias es sobre espacios vectoriales. Gracias de antemano.



David
el 21/11/16Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)