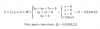-


Antonio Silvio Palmitano
el 18/11/16Presentemos las condiciones que cumplen los vectores pertenecientes al subespacio vectorial U como un sistema de ecuaciones:
5z = 0, de donde puedes despejar: z = 0
4y + 2z = 0
5x + 4y + 7z = 0,
sustituyes en la segunda y en la tercera ecuación, resuelves términos y queda el sistema:
4y = 0, de donde puedes despejar: y = 0
5x + 4y = 0,
sustituyes en la segunda ecuación, resuelves término y queda la ecuación:
5x = 0, de donde puedes despejar: x = 0,
luego, observa que t no quedó restringido (quedó "libre"), por lo que puede tomar cualquier valor real.
Luego, un vector genérico del subespacio vectorial U puede escribirse:
u = <x,y,z,t> = reemplazamos componentes = <0,0,0,t> = extraemos factor escalar = t•<0,0,0,1>, con t ∈ R.
Luego, una base del subespacio vectorial U estará formada por un vector que sea múltiplo escalar de <0,0,0,1>,
como muestra la opción (a): βU = {<0,0,0,2>}, ya que el vector es el doble del vector <0,0,0,1>.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 18/11/16Observa que el dominio de la función es el conjunto de los números reales: D = R, y que la función es continua en todos los puntos de su dominio.
Luego, puedes plantear la expresión de la función derivada por medio de la regla del cociente, lo haces y queda:
f ' (x) = (3ex - (3x+1)ex) / (ex)2, luego, observa que la función derivada también está definida para todos los puntos del dominio de la función.
Luego, planteamos la condición de punto crítico (posible máximo o posible mínimo):
f ' (x) = 0, sustituimos y queda:
(3ex - (3x+1)ex) / (ex)2 = 0, hacemos pasaje de divisor como factor, resolvemos el segundo miembro y queda:
3ex - (3x+1)ex = 0, extraemos factor común ex y queda:
ex( 3 - (3x+1) ) = 0, luego, recuerda que el factor exponencial es estrictamente mayor que cero, por lo que lo pasamos como divisor, resolvemos y queda:
3 - (3x+1 = 0, distribuimos el agrupamiento y queda:
3 - 3x - 1 = 0, hacemos pasaje de términos, reducimos términos semejantes y queda:
- 3x = - 2, dividimos por -3 en ambos miembros y llegamos a:
x = 2/3.
Luego, podemos comparar con puntos testigos, uno menor y otro mayor que el punto crítico:
f(0) = 1
f(2/3) = ( 3(2/3) + 1)/e2/3 = 3/e2/3 ≅ 1,5403
f(1) = ( 3*1 + 1)/e1 = 4/e ≅ 1,4715
Luego, como el valor de la función en el punto crítico es mayor que los valores en los puntos testigos,
concluimos que la gráfica de la función presenta un máximo en x = 2/3.
Espero haberte ayudado.
-
Buenas por favor alguien que me pueda ayudar en este ejercicio

se que x toma el valor de x = r cos θ
y que y toma el valor de y = r sen θ , pero no se como aplicar aquí en derivadas
por favor de antemano muchas gracias a quien se tome la molestia de ayudarme


David
el 21/11/16Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-


Antonio Silvio Palmitano
el 18/11/16Para el segundo ejercicio:
Observa que: (x + 1/x)2 = x2 + 2x(1/x) + (1/x)2= x2 + 2 + 1/x2, luego tenemos, a partir de la igualdad entre los miembros remarcados:
(x + 1/x)2 - 2 = x2 + 1/x2.
Luego, pasamos a la expresión de la función:
f(1+1/x) = x2 + 1/x2 = (x + 1/x)2 - 2, luego, sustituimos el argumento y tenemoss finalmente: f(x) = x2 - 2, (|x| ≤ 2).
Para el tercer ejercicio:
Observa que x = (1/x)-1, luego sustituimos en la expresión de la función y queda:
f(1/x) = x + √(1+x2) = (1/x)-1 + √( 1 + ( (1/x)-1 )2 ), luego sustituimos el argumento y tenemos:
f(x) = x-1 + √( 1 + (x-1)2 ) = x-1 + √( 1 + x-2 ) = 1/x + √( 1 + 1/x2 ) (x > 0).
Espero haberte ayudado.
-
Buenas un favor alguien que me pueda ayudar con este ejercicio

no se si despejar x o y o si debo despejar x o y de u y v porfavor alguien que me ayude


David
el 21/11/16Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
Un deposito para granos es construido acoplando a un cilindro circular recto, de altura h metros y radio r metros, una semiesfera de radio r metros. Si el area total de la superficie del deposito es 20π metros cuadrados, determine los valores de r y h para que su volumen sea maximo.
Pregunta:¿ tengo que quitarle la tapa superior del cilindro y la de la semiesfera(en la formula del area)? (lo digo porque como es un deposito para granos y me resulta dudoso que le ponga ambas tapas)
psdta: si fuese asi en el volumen tambien tengo que quitarle algo?, gracias de antemano :D


Antonio Silvio Palmitano
el 18/11/16Vamos con ayudas para las expresiones de áreas y volúmenes que necesitas.
Consideramos que la pared cilíndrica y la tapa semiesférica son las que debemos construir con chapa.
Luego, tienes para el área:
A = Ac + As
Área cilíndrica: Ac = 2πrh
Área semiesférica: As = (1/2)(4)πr2 = 2πr2
No consideramos la tapa superior del cilindro, que coincidiría con la base de la semiesfera, ya que el interior del depósito está vació.
Luego, tienes para el volumen:
V = Vc + Vs
Volumen cilíndrico: Vc = πr2h
Volumen semiesférico: Vs = (1/2)(4/3)πr3 = (2/3)πr3
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 18/11/16Observa que la expresión del elemento general de la sucesión podemos escribirla:
an = √(n2 + 1)sen(nn)/√(n2) = √( (n2 + 1)/n2 )sen(nn) = √(1 + 1/n2)sen(nn).
Luego, planteamos el limite de la expresión para n tendiendo a +infinito:
Lím(n-->+inf) an = Lïm(n-->+inf) √(1 + 1/n2)sen(nn) = Lïm(n-->+inf) √(1 + 1/n2) * Lím(n-->+inf) sen(nn) = no existe, porque:
el primer límite: Lïm(n-->+inf) √(1 + 1/n2) = 1,
el segundo límite: Lím(n-->+inf) sen(nn) no existe, porque la expresión oscila entre -1 y 1, y está acotada entre -1 y 1.
Luego, la opción (b) es la correcta.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 18/11/16Comencemos.
Observa que 512 =29, luego tienes: log2512 = log2(29)= 9log22 = 9•1 = 9;
luego, la expresión queda:
K = ( log√2 log39 )3,
observa que 9 = 32,luego tienes: log39 = log332 = 2log33 = 2•1 = 2;
luego la expresión queda:
K = ( log√2 2 )3,
observa que 2 = (√2)2, luego tienes: log√22 = log√2(√2)2 = 2 log√2√2 = 2•1 = 2;
luego la expresión queda:
K = 23 = 8.
Espero haberte ayudado.