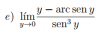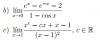-
alguien me puede ayudar por favor?,en serio necesito ayuda ya que tengo examen el lunes :( , estuve haciendolo pero me di cuenta que -1 no deberia pertenecer al primer intervalo, entonces probe con redefinir la funcion en x->-1 pero me sale que es de tipo discontinua inevitable :(.gracias!!!.

-


Antonio Silvio Palmitano
el 19/11/16Comencemos por plantear la continuidad en el punto de corte x = 1.
1) f(1) = β/(12+1) = β/2 (observa que 1 pertenece al intervalo del segundo trozo).
2) Límites laterales:
Lím(x->1-) f(x) = Lím(x->1-) (αx+1) = α + 1.
Lím(x->1+) f(x) = Lím(x->1+) β/(x2+1) = β/2
luego, para que exista el límite deben ser iguales los límites laterales y coincidir con el valor de la función en el punto de estudio, por lo que tenemos la ecuación:
α + 1 = β/2, multiplicamos por 2 en todos los términos de la ecuación, hacemos pasajes de términos y queda:
2α - β = - 2.
Una forma de plantear la existencia de la derivada en el punto de estudio es plantear las expresiones de las derivadas laterales:
f-' (x) = α
f+' (x) = - 2βx/(x2+1)2
Luego tomamos sus límites:
Lím(x->1-) f ' (x) = α
Lím(x->1+) f ' (x) = - β
luego, para que exista el límite deben ser iguales los limites laterales, por lo que tenemos la ecuación: α = - β, hacemos pasaje de término y queda:
α + β = 0.
Luego, solo nos queda resolver el sistema formado por las dos ecuaciones remarcadas, lo haces y su solución queda:
α = -2/3, y β = 2/3.
Luego, puedes apreciar que los límites de las derivadas laterales para x tendiendo a 1 nos quedan iguales a -2/3, por lo que tenemos:
f ' (1) = -2/3, que es igual a la pendiente de la recta tangente a la gráfica de la función en el punto de abscisa x = 1.
Espero haberte ayudado.
-
Buenas tardes, tengo un problemilla tengo examen el martes de matematicas y estoy más que perdida, el problema que tengo es que no me entero de lo que ''explica'' la profesora, tambien es que llevo 6 años sin estudiar matematicas y me meti en bachillerato de ciencias, las dudas que tengo es de los Numeros Reales( conjunto de los numeros reales, representacion de los numeros reales en la recta real, conjuntos en la recta real, conjuntos acotados en la recta real, notacion cientifica y orden de magnitud, radicales, operaciones con radicales y reacionalización de denominadores) y del Algebra I: Polinomios. Ecuaciones y Sisemas ( Teorema del resto y teorema del factor, descomposición factorial de un polinomio, fracciones algebraicas, operaciones con fracciones algebraicas, descomposicion de una fraccion algebraica en suma de fracciones simples, ecuaciones de segundo grado resolucion, ecuadiones de grado superior a dos, ecuaciones irracionales, sistemas de ecuaciones de segundo grado, sistemas de ecuaciones lineales, sistemas equivalentes y metodo de Gauss). Eso seria lo que me entra en el examen, me entere ayer y ahora acabo de encontrar esta pagina. Espero que me podais ayudar. Gracias

Ángel
el 19/11/16Lo que puede ser más efectivo en este caso es que entres aquí:
http://www.unicoos.com/cursos/1-bachiller/matematicas
y te tires hoy, mañana y pasado viendo los videos de los bloques que sean de tu interés e intentándolos resolver tú.
En cuanto tengas una duda la preguntas por aquí
Suerte!
-


David
el 21/11/16Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
Hola, me podrían ayudar con los pasos para resolver esta ecuación? Muchas gracias
x2- 2x = 0 la parte de arriba está dividida por la de abajo y todo es igual a 0, solo que no sé bien como escribirlo
x2- 2x + 1

Ángel
el 19/11/16x2- 2x/ x2- 2x + 1= 0
Primero resolvemos la ecuación de segundo grado del denominador y nos queda que x1=x2=1, entonces x2- 2x + 1= (x-1)(x-1)...esto quiere decir que el denominador valdrá cero si x=1, lo cuál indeterminaría la solución. En conclusión: "x no puede valer 1"
Ahora busquemos los valores que puede tomar:
x2- 2x/ x2- 2x + 1= 0
factorizamos:
x(x-2)/(x-1)(x-1)= 0
el denominador que está dividiendo pasa al otro lado multiplicando
x(x-2)= 0*(x-1)(x-1)
...
x(x-2)=0
x1= 0 y x2=2
como x1= 0≠ 1 y x2=2≠ 1, nos aseguramos que estas soluciones son válidas (ya que 1 era el valor que NO podía tomar, por anular el denominador)
-
Hola de nuevo, tengo un problema con los máximos y minimos dada la función f (x)= x^2/3 en I=(-2,3), ya derive la función y me queda 2/3x^1/3, y se que hay que buscar numeros donde la cual se haga 0, pero de ahi no paso, el profesor habla de los puntos fronterizos, estacionarios y singulares, y quiero un metodo un poco mas sencillo o entender la comprensión de como sacar dichos puntos gracias de ante mano.


Antonio Silvio Palmitano
el 19/11/16Por favor, ¿puedes confirmar si el intervalo I = (-2,3) es abierto (como has escrito) o cerrado?
Si el intervalo es tal cuál como has escrito, comencemos:
La expresión de la función derivada queda (observa que debes corregir el exponente):
f ' (x) = (2/3)x-1/3 = 2 / ∛(x), que se indetermina para x = 0 que pertenece al intervalo.
Luego, planteamos la condición de punto crítico (posible máximo o posible mínimo):
f ' (x) = 0, sustituimos y queda:
2 / ∛(x) = 0, hacemos pasaje de divisor como factor y queda:
2 = 0•∛(x), resolvemos el segundo miembro y queda:
2 = 0, que es una identidad absurda, por lo que concluimos que no hay puntos críticos.
Para el punto en que se indetermina la expresión de la función derivada (x = 0), estudiamos los valores que toma la función para puntos a sus lados:
f(-1) = (-1)2/3 = 1
f(0) = 02/3 = 0
f(1) = 12/3 = 1
Luego, concluimos que la función presenta un mínimo en x = 0, y vemos también que la función es continua en dicho punto, pero que no es derivable en dicho punto.
Y como el intervalo es abierto, tenemos que los extremos no pertenecen a él, por lo que no podemos evaluarlos en la expresión de la función, que no presenta máximo en el intervalo.
Espero haberte ayudado.


Itzel Sustaita
el 19/11/16Hola, si disculpa me equivoque al escribir, es con intervalos cerrados, pero el resultado que me diste son los mismos a como lo hizo mi profesor, solo aqui que dijo que el minimo era 1 y el maximo 1.58, pero solo otra dudita más pasos claves a seguir para la resolución de ejercicios como este, ya se que hay que derivar la función y de ahi buscar en donde no se hace 0, pero en este caso no se puede factorizar ni nada, y ahi es donde me pierdo, se que en este ejercicio no debe ser 0 en el denominador pero de ahi ya no se como sacar los otfos intervalos, y para ser honesta la táctica que usa mi profesor no le entiendo, igual muchas gracias por la respuesta.
-
alguien sabe solucionar este problema: hallar la ecuación paramétrica que pasa por el punto A(3,0,-1) y que su vector director es perpendicular al vector director de t=(x,y,z)=(1,-5,3) + λ(-2,-5,4)


Antonio Silvio Palmitano
el 19/11/16Por favor, verifica que el enunciado esté completo.
Con los datos que tienes en el enunciado, vemos que el punto de coordenadas A(3,0,1) pertenece a la recta t, y le corresponde el valor del parámetro: λ = -1.
Luego, como estamos en R3, tenemos que existen infinitos vectores perpendiculares al vector director de la recta t: u = <-2,-5,4>, por lo que tendremos un conjunto de infinitas rectas que pasan por el punto A, con sus vectores directores perpendiculares al vector u ( a este conjunto se lo suele llamar "haz de rectas" con centro en el punto A).
Luego, planteamos el vector: v = <a,b,c>, y como debe ser perpendicular al vector u, planteamos la condición de perpendicularidad entre vectores no nulos:
u•v = 0, sustituimos y queda:
<-2,-5,4> • <a,b,c> = 0, desarrollamos y queda la ecuación:
- 2a - 5b + 4c = 0, luego despejamos una de las incógnitas, por ejemplo:
a = - 5b/2 + 2c, luego sustituimos en la expresión del vector v y queda:
v = < - 5b/2 + 2c , b , c >, con b y c números reales distintos de cero (observa que con elegir arbitrariamente los valores para b y c ya tienes un vector perpendicular al vector u).
Luego, planteamos la ecuación vectorial paramétrica y queda:
< x , y , z > = < 3 , 0 , - 1 > + λ< - 5b/2 + 2c , b , c >, con b ∈ R, c ∈ R, b ≠ 0, c ≠ 0, y el parámetro λ ∈ R.
Tal como indicamos antes, esta ecuación corresponde al haz de rectas perpendiculares a la recta t que pasan por el punto A.
Como ejemplos, podemos determinar una de las rectas del haz, y para ello elegimos: b = 2, c = 1, luego reemplazamos y queda:
< x , y , z > = < 3 , 0 , - 1 > + λ< -3 , 2 , 1 >;
y si elegimos otros valores, como: b = 4, c = 0, reemplazamos y queda:
< x , y , z > = < 3 , 0 , - 1 > + λ< -10 , 4 , 0 >;
y así podríamos continuar, y obtendríamos para cada par de valores de b y c una recta distinta que forma parte del haz.
Espero haberte ayudado.