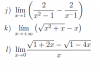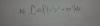Por favor, dirige tu consulta al Foro de Física para que los colegas puedan ayudarte.

Recuerda que para poder aplicar la Regla de L'Hôpital, debes tener un cociente en el argumento del límite, que debe ser indeterminado.

i) Observa que la expresión en el argumento del límite puede escribirse:

f(x) = 2 / (x+1)(x-1) - 2/(x-1) = extraemos denominador común:

= ( 2 - 2(x+1) ) / (x+1)(x-1) = distribuimos en el numerador, reducimos términos semejantes y queda:

= - 2x / (x+1)(x-1).

Luego pasamos al cálculo del límite:

L = Lím(x-->1) ( - 2x / (x+1)(x-1) ) = infinito (observa que el numerador tiende a -2, y que el denominador tiende a 0, y que no fue necesario aplicar la Regla de L'Hôpital).

j) Observa que en la expresión de la función podemos multiplicar por la expresión "conjugada", y queda:

g(x) = ( √(x² + x) - x )( √(x² + x) + x ) / ( √(x² + x) + x ), distribuimos en el numerador, operamos y queda:

= (x² + x - x² ) / ( √(x² + x) + x ) = cancelamos términos opuestos en el numerador y queda:

= x / ( √(x² + x) + x ), luego puedes continuar la tarea, y calcular el límite con la Regla de L'Hôpital.

k) Podemos multiplicar y dividir por la expresión "conjugada" del numerador, y la expresión de la función puede escribirse:

h(x) = ( √(1+2x) - √(1-4x) )( √(1+2x) + √(1-4x) ) / x( √(1+2x) + √(1-4x) ) =

distribuimos en el numerador, operamos y queda:

= ( 1 + 2x - (1 - 4x) ) / x( √(1+2x) + √(1-4x) ) = distribuimos, reducimos términos semejantes en el numerador y queda

= 6x / x( √(1+2x) + √(1-4x) ) = simplificamos y queda:

= 6 / ( √(1+2x) + √(1-4x) ), luego pasamos al cálculo del límite:

L = Lím(x-->0) h(x) = Lím(x-->0) 6 / ( √(1+2x) + √(1-4x) ) = 6/2 = 3,

observa que el cálculo es directo, y que no resultó necesario aplicar la Regla de L'Hôpital para resolver el límite.

Espero haberte ayudado.

Aylen va 

no le eh entendido mucho :(

Para estudiar la continuidad de la función en el punto de coordenadas A(0,0), observa:

1) La función no está definida en el punto, ya que su denominador toma el valor cero para el punto de estudio.

2) Para analizar el límite, ensayamos caminos:

a) x = 0, luego nos queda: La = Lím(y-->0) 0/√(0² + y²) = Lím(y-->0) 0/√(y²) = Lím(y-->0) 0/|y| = 0.

b) y = 0, luego nos queda: Lb = Lím(x-->0) x²/√(x² + 0²) = Lím(x-->0)  x²/√(x²) = Lím(x-->0)  x²/|x| = Lím(x-->0) |x|²/|x| = Lím(x-->0) |x| = ± 1.

Luego, como los límites no coinciden, tenemos que el límite de la función para (x,y) tendiendo a (0,0) no existe.

3) Como el límite no existe, concluimos que la función presenta una discontinuidad esencial (inevitable) en el punto de estudio A(0,0).

Espero haberte ayudado.

Va Laura 

En el límite por el segundo camino, he escrito con error el numerador: debe ser x (en lugar de x² como conigné erróneamente), y la última expresión para calcular el límite debe ser: x/|x| = ± 1.

Disculpa el error involuntario.

Tienes proporcionalidad compuesta directa entre la masa del envío y la distancia, con el costo.

Partimos de:

75 Kg    350 Km    30 e

a) Planteamos:

75 Kg    350 Km    30 e

30 Kg    210 Km    x

Luego:

75/30 * 350/210 = 30e/x, simplificamos en cada factor:

5/2 * 5/3 = 30e/x, resolvemos el primer miembro:

25/6 = 30e /x, hacemos pasajes de factores y divisores:

x = 6*30e / 25, resolvemos:

x = 180e / 25 = 7,20 e.

b) Planteamos:

75 Kg    350 Km    30 e

  y           160 Km    68 e

Luego:

75Kg/y * 350/160 = 30/68, y puedes continuar la tarea.

c) Planteamos:

  75 Kg    350 Km    30 e

100 Kg        z         130 e

Luego:

75/100 * 350Km/z = 30/130, y puedes continuar la tarea.

Espero haberte ayudado.

Observa que el límite del valor absoluto del término general, para n tendiendo a +infinito queda:

Lím(n-->+inf) |a_n| = Líjm(n-->+inf) n² = + inf, por lo que la serie es divergente (si hubiese sido igual a cero, tendríamos que continuar estudiando la convergencia o divergencia de la serie, pero como no es igual a cero, concluimos que no es divergente).

Espero haberte ayudado.

Yo lo veo así 

Asi Aitana 

Despejamos en la primera ecuación: logx = 5 - 3logy (*),

sustituimos en la segunda ecuación y queda:

5 - 3logy - logy = 3, hacemos pasajes de términos, reducimos términos semejantes y queda:

- 4logy = - 2, hacemos pasaje de factor como divisor, simplificamos a la derecha y queda:

logy = 1/2 (**), luego componemos con la función inversa del logaritmo decimal y queda:

y = 10^1/2= √(10).

Luego reemplazamos el valor señalado (**) en la expresión señalada (*) y queda:

logx = 5 - 3(1/2), resolvemos el segundo término a la derecha y queda:

logx = 5 - 3/2, resolvemos a la derecha y queda:

logx = 7/2, luego componemos con la función inversa del logaritmo decimal y queda:

x = 10^7/2 = √(10⁷).

Espero haberte ayudado.

Lo de las cortaduras no se lo que es, al menos con ese nombre 

1/2k, acuerdate de lo del producto de los extremos sobre el producto de los medios

mmm esto es duda universitaria, pero el primer rango seria sobre el eje X, el segundo sobre el eje Y, 

pero te recomendaria quizas usar cordenadas polares, se te haria mas facil quiza

La notación como producto cartesiano R = [-1,1]x[0,1], equivale a los intervalos: -1≤x≤1, 0≤y≤1. Luego, pasamos a la integral doble:

I = ∫∫_R(x² + y²)dydx = integramos parcialmente con respecto a y, y queda:

= ∫ [x²y + y³/3]dx = evaluamos para y entre 0 y 1 y queda:

= ∫ ( x²  + 1/3 )dx = integramos con respecto a x:

= [ x³/3 + 1x/3 ] = evaluamos para x entre -1 y 1 y queda:

= (1/3 + 1/3) - (-1/3 - 1/3) = 2/3 - (-2/3) = 4/3.

Espero haberte ayudado.