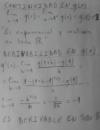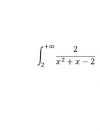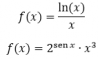-
Buenas noches, necesito que me ayuden con esta integral y me digan porqué la sustitución que está rodeada de rojo, no entendí de donde salió o será que está mal?


Antonio Silvio Palmitano
el 14/11/16Observa que te proponen la sustitución:
√(4 + x2) = 2secθ , de donde tienes: (1/2)√(4 + x2) = secθ (*), y también tienes:
4 + x2 = 4sec2θ, luego tienes al diferenciar:
2xdx = 8secθ*sec2θ*senθ* dθ = 8sec2θ*tanθ*dθ, luego despejas y queda (empleamos el primer miembro y el último miembro de la cadena de igualdades:
xdx = 4sec2θ*tanθ*dθ
Luego, pasas a sustituir:
I = ∫ ( xdx / √(4 + x2) ) = ∫ ( 4sec2θ*tanθ*dθ / 2secθ ) = 2 ∫ ( secθ*tanθ*dθ)
Luego, puedes plantear la sustitución:
y = secθ = 1/cosθ, luego su diferencial queda:
dy = ( -1/cos2θ ) * (-senθ)*dθ = ( senθ/cosθ )( 1/cosθ)dθ = tanθ*secθ*dθ,
luego sustituyes y la integral queda:
I = 2 ∫ dy = y + C = 2secθ + C = .sustituimos a partir de la ecuación señalada (*) = 2(1/2)√(4 + x2) + C = √(4 + x2) + C.
Espero haberte ayudado.
-
 Buenas noches, me piden que decida si es continua, el problema es que no puedo asegurar la existencia de limites, mi respuesta sería que no puedo decir si es continua o discontinua ya que no puedo asegurar la existencia del limite?
Buenas noches, me piden que decida si es continua, el problema es que no puedo asegurar la existencia de limites, mi respuesta sería que no puedo decir si es continua o discontinua ya que no puedo asegurar la existencia del limite?

Antonio Silvio Palmitano
el 14/11/16Observa que la expresión del primer trozo la puedes escribir:
(x2 +y2 + 2xy2)/(x2 + y2) = luego agrupas los dos primeros términos en el numerador, distribuyes el denominador y queda:
= (x2 +y2)/(x2 +y2) + 2xy2/(x2 +y2) = 1 + 2xy2/(x2 +y2).
Luego, puedes continuar la tarea del cálculo del límite para (x,y) tendiendo a (0,0), y observa que el primer término es constante, y que el segundo tiene límite igual a cero, y podrás demostrarlo con el teorema de acotación (o de encaje, o "del sandwich"), como seguramente has hecho en clase en otros ejercicios.
Espero haberte ayudado.
-
ALguien me ayuda con esta integral impropia. la hago y me da que diverge. pero en la solucion es que converge a log 4.


Antonio Silvio Palmitano
el 14/11/16Vamos a aplicar el método de las fracciones parciales (observa que las raíces del denominador son 1 y -2):
2/(x-1)(x+2) = a/(x-1) + b/(x+2) = ( a(x+2) + b(x-1) ) / (x+2)(x-1)
Luego comparamos numeradores y queda la igualdad entre polinomios:
2 = a(x+2) + b(x-1)
que es válida para a = 2/3. y b = -2/3.
Luego, la integral puede escribirse:
I = (2/3) ∫ ( 1/(x-1) - 1/(x+2) )dx = (2/3)( ln|x-1| - ln|x+2| ) = (2/3)ln| (x-1)/(x+2) | (no consignamos la constante de integración porque estamos tratando con una integral definida).
Luego, evaluamos con Regla de Barrow, entre 2 y a:
I = (2/3)ln| (a-1)/(a+2) | - (2/3)ln| 1/4 | = (2/3)ln| (a-1)/(a+2) | + (2/3)ln(4)
Luego, tomamos el límite para a tendiendo a +infinito, observa que el argumento del logaritmo en el primer término tiende a cero, y llegamos a:
I = (2/3)ln(4)
Por lo que concluimos que la integral es convergente.
Espero haberte ayudado.
-
Hola Unicoos,
¿Me ayudais con ésta inecuación?
Gracias!



Antonio Silvio Palmitano
el 14/11/16Puedes aplicar la sustitución (cambio de incógnita): cosx = w, observa que w debe tomar valores comprendidos entre -1 y 1 (*), sustituyes y queda la inecuación:
2w2 + 5w - 3 > 0, luego observa que la expresión polinómica tiene raíces 1/2 y -3, luego factorizamos y queda:
2(w - 1/2)(w + 3) > 0, luego dividimos por 2 en ambos miembros y queda:
(w - 1/2)(w + 3) > 0, lo que nos conduce a dos opciones:
a) w - 1/2 > 0 y w + 3 > 0, lo que nos conduce a w > 1/2, y con la consideración señalada (*) tenemos: w ∈ (1/2,1]
b) w - 1/2 < 0 y w + 3 < 0, lo que nos conduce a w < -3, y con la consideración señalada (*) tenemos w ∈ ∅
Luego, tenemos finalmente: w ∈ (1/2,1] u ∅ = (1/2,1]
Luego, sustituimos, planteamos la desigualdad para la expresión de w y queda:
1/2 < cosx ≤ 1, luego componemos con la función inversa del coseno y tenemos dos opciones:
1) 0 ≤ x < π/3 ∨ 5π/3 < x ≤ 2π, luego con notación de intervalo; x ∈ [ 0 , π/3 ) u ( 5π/3 , 2π ]
Espero haberte ayudado.
-
Ayuda con esta derivada.
6tag23x + 2 = 4


Antonio Silvio Palmitano
el 14/11/16Haces pasaje de término y queda:
6tag23x = 2, haces pasaje de factor como divisor y queda:
tag23x = 1/3 = 3/9, haces pasaje de potencia como raíz y quedan dos opciones:
a) tag3x = +√(3)/3, que nos conduce a dos opciones:
a1) 3x = 30° + 360°*k, divides por 3 en todos los términos y queda:
x = 10° + 120°*k, con k ∈ ℤ
a2) 3x = 210° + 360°*k, divides por 3 en todos los términos y queda:
x = 70° + 120°*k, con k ∈ ℤ
b) tag3x = -√(3)/3, que nos conduce a dos opciones:
b1) 3x = 1500° + 360°*k, divides por 3 en todos los términos y queda:
x = 50° + 120°*k, con k ∈ ℤ
a2) 3x = 330° + 360°*k, divides por 3 en todos los términos y queda:
x = 110° + 120°*k, con k ∈ ℤ
Espero haberte ayudado.
-

Ángel
el 14/11/16Derivada de un cociente=[derivada numerador*denominador - numerador*derivada denominador]/denominador2
f´(x)= [1/x*x-ln(x)]/x2= [1-ln(x)]/x2
Derivada de una multiplicación= derivada primero*segundo + primero*derivada segundo
f´(x)=2senx* cos x * Ln2*x3+2senx*3x2 = 2senx*x2(cos x * Ln2*x+ 3)
((recuerda que si f(x)= au, entonces f´(x)= au* Ln a * u´))