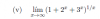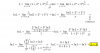-
Jose Manuel
el 5/11/16
Alguien me dice como obtengo b en este sistema de congruencias?
-
Daniel
el 5/11/16Ayuda con esta integral porfavooooor
Antonio Silvio Palmitano
el 5/11/16Has planteado correctamente los límites de integración y el cambio de cordenadas. Observa que el argumento de la raíz en la expresión de la función queda.
16 - r:²(oos:²θ + sen:²θ) = 16 - r:², luego al integral queda:
V = ∫∫ V(16 - r:²)rdrdθ , con 0 ≤ θ ≤ 2π y 0 ≤ r ≤ 2.
Observa que la integral para r puedes resolverla con la sustitución: w = 16 - r:², y luego continuar la tarea.
Espero haberte ayudado.
-
Ron Rc
el 5/11/16me podrian ayudar con este ejercicio porfa ? :( no entiendo muy bien que tengo que hacer :/
-
Sofía :)
el 5/11/16Hola!! Queria pedirles ayuda sobre esta ECUACION:
(X +1) : 2 = 2 X + 10
Podrían hacermelo? porque no se si todo lo que esta en el parentesis se divide por 2 o si ese ".2" pasa multiplicando.
Antonio Silvio Palmitano
el 5/11/16Puedes comenzar por multiplicar por 2 en todos los términos de la ecuación y queda:
x + 1 = 4x + 20, haces pasajes de términos y queda:
x - 4x = 20 - 1, resuelves en ambos miembros y queda:
- 3x = 19, multiplicamos por -1/3 en ambos miembros, resolvemos a la derecha y queda:
x = -19/3.
Con respecto a tu pregunta, observa:
el denominador de la izquierda es común para todo el primer miembro, por lo que podrías haber comenzado:
x + 1 = 2(2x + 10);
o, si prefieres, puedes distribuir el denominador y comenzar con:
x/2 + 1/2 = 2x + 10.
Luego, con cualquiera de las formas, llegarás al mismo resultado. Haz el intento para verificar, y de paso practicas.
Espero haberte ayudado.
-
Cindy Entes
el 5/11/16Buenas, tengo un problema con esta integral: 1/(1+x^4)dx, agradecería que alguien me la explicara. =)
-
Eleo Romario Huayhua Paco
el 5/11/16Hola, necesito ayuda con este ejercicio de ante mano Gracias!.
-
Carmen Vega
el 5/11/16Buenas tardes, alguien me podría ayudar a despejar la Z de esta ecuación? 2.C-1Z.C+I3=B.Bt
gracias!
-
Maria del castillo
el 5/11/16 -
Alex Domínguez
el 5/11/16Hola, me ayudan con este ejercicio ? Gracias
Gracias
David
el 7/11/16Te sugiero estos vídeos, todos los de esta lección.. ALGEBRA Matriz de Cambio de Base 01 A partir de ahí, me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. Lo siento de corazón… Espero lo entiendas
-
Miguel Lantigua Rodríguez
el 5/11/16Buenas Tardes Unicoos,
¿Alguien me puede ayudar con este ejercicio de Optimización?
- De todos los prismas rectos de base cuadrada y tales que el perímetro de una cara lateral es de 30 cm, halla las dimensiones del que tiene su volumen máximo.
Gracias
