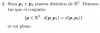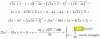-
emerson acosta
el 6/11/16Me dicen que determine si es o no es un espacio vectorial con la operaciones dadas:
1.- El conjunto V={(x,y)/x>0 ∧ y>0} Con las operaciones vectoriales usuales de adicion y multiplicacion por un escalar.
No entiendo muy bien el tema de espacios vectoriales, lo menos este ejercicio no se como hacerlo.
-
Isa Garcia Prieto
el 6/11/16 -
ALOFRE
el 6/11/16Hola, agradecería ayuda para este problema de identidades notables, que, a mi parecer no cumple las fórmulas estudiadas; aunque probablemente se trate de que he pasado algo por alto.
- Descompón estas expresión en factores: -x^2 y^2 -9y^2 -6xy^2 No entiendo como pueden ser todos los monomios negativos... gracias.
Tora Kevin Yack Quispe Tapia
el 6/11/16 -
Jose Manuel
el 6/11/16
Alguien me lo resuelve?,tengo examen mañana ayuda por favor
Tora Kevin Yack Quispe Tapia
el 6/11/16
David
el 7/11/16Se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado, De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
Sobre todo, si como en este caso, "debemos" hacer una excepción pues tu duda SE SALE DE LOS CONTENIDOS DE UNICOOS. Abrazos -
Valeria Galindo
el 6/11/16Hola, alguien me podría explicar que es lo que debo demostrar en este ejercicio por favor
-
Valeria Galindo
el 6/11/16 -
Javier García
el 6/11/16Me pueden decir en que me he equivocado? Al hacer la raiz cuadrada en la formula de 2º grado me da decimales y no encuentro el error...
Alex Domínguez
el 6/11/16 -
Ana María Canales
el 6/11/16Hola. Estoy cursando 2º de bachillerato de ciencias sociales y tengo una duda sobre ecuaciones matriciales. Si me dan una ecuación que es por ejemplo: XA^2=B , al multiplicar esa matriz A al cuadrado por su inversa, ¿desaparecería la A al salir la identidad o seguiría habiendo una A?
Gracias de antemano.
Antonio Silvio Palmitano
el 6/11/16Observa que puedes escribir la ecuación matricial en la forma (asumimos que la matriz A es invertible):
XAA = B, luego multiplicas en ambos miembros por la matriz inversa de A del lado derecho y queda:
XAA*A^(-1) = B*A^(-1), luego como el producto de una matriz por su matriz inversa es igual a la matriz identidad, queda:
XA*I = B*A^(-1), luego, como la matriz identidad es neutra para el producto de matrices queda:
XA = B*A^(-1), luego multiplicas en ambos miembros por la matriz inversa de A del lado derecho y queda:
XA*A^(-1) = B*A^(-1)*A^(-1), luego como el producto de una matriz por su matriz inversa es igual a la matriz identidad, queda:
X*I = B*A^(-1)*A^(-1), luego, como la matriz identidad es neutra para el producto de matrices queda:
X = B*A^(-1)*A^(-1), luego expresamos el producto de las dos últimas matrices de la derecha como potencia y queda:
X = B*( A^(-1) )², luego, por propiedad de la inversa de una potencia de una matriz queda:
X = B*(A²)^(-1).
Espero haberte ayudado.
-
CJB
el 6/11/16 -
jose
el 6/11/16
