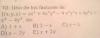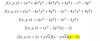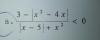-
Buen día me gustaría obtener la ecuación de la hipérbola respecto a este ejercicio, muchas gracias!!


Antonio Silvio Palmitano
el 4/11/16Ubica un sistema de coordenadas cartesiano con origen en el punto medio del diámetro más pequeño, con eje de abscisas OX paralelo al piso, y eje de ordenadas OY coincidente con el eje de simetría de la estructura. (observa que el origen de coordenadas está ubicado a una altura de 84 metros con respecto al piso).
Observa que tienes que los vértices reales de la hipérbola son los puntos de coordenadas: A1(-24,84) y A2(24,84), con lo que tienes que la longitud del semieje real de la hipérbola es: a = 24, y que su ecuación queda planteada:
x²/24² - y²/b² = 1.
Luego, observa que el punto de contacto entre la base de la estructura y el suelo (consideramos el punto de la derecha), tiene coordenadas: P(50,-84) (recuerda cómo hemos ubicado el origen de coordenadas de nuestro sistema cartesiano), reemplazas en la ecuación de la hipérbola y queda:
50²/24² - (-84)²/b² = 1, haces pasajes de términos y queda:
50²/24² - 1 = (-84)²/b², resolvemos potencias, simplificamos a la izquierda y queda:
625/144 - 1 = 7056/b², resolvemos a la izquierda y queda:
481/144 = 7056/b², hacemos pasajes de factores como divisores y de divisores como factores y queda:
b² = 7056*144/481, hacemos pasaje de potencia como raíz, distribuimos entre factores y resolvemos a la derecha:
b = 84*12/V(481), resolvemos en el numerador, racionalizamos el denominador y queda:
b = 1008*V(481)/481 = 45,96 (aproximadamente).
Luego, la ecuación de la hipérbola queda (con valores aproximados):
x²/24² - y²/45,96² = 1.
Luego, para los puntos A y B de la estructura que se encuentran a 120 de altura sobre el piso, observa que la ordenada para ambos es y = 36 (recuerda que el origen de coordenadas de nuestro sistema cartesiano se encuentra a 84 de altura sobre el piso), reemplazamos en la ecuación de la hipérbola y queda:
x²/24² - 36²/45,96² = 1, hacemos pasaje de término y queda:
x²/24² = 1 + 36²/45,96², resolvemos potencias y queda:
x²/576 = 1 + 1296/2112,32, resolvemos a la derecha y queda:
x²/576 = 1,61 (aproximadamente), hacemos pasaje de divisor como factor, resolvemos a la derecha y queda:
x² = 929,40, hacemos pasaje de potencia como raíz, resolvemos a la derecha y tenemos dos opciones (recuerda que las ordenadas de ambos puntos están referidas al sistema de ejes cartesianos con origen de coordenadas ubicados a 84 m de altura sobre el nivel del piso):
a) x = -30,49, de donde tenemos que las coordenadas del punto A son: A(-30,49,36);
b) x = 30,49, de donde tenemos que las coordenadas del punto B son: B(30,49,36).
Espero haberte ayudado.
-
Buenas! No consigo entender este ejercicio: tengo que averiguar si (x,y,z) es un subespacio de R3 tal que x+y=z, x+z=y
Espero que me podáis ayudar, gracias!!!!

Antonio Silvio Palmitano
el 4/11/16Observa que tienes dos condiciones, por lo que puedes elegir a una de las componentes de los vectores como parámetro, por ejemplo:
Sustituimos la expresión para z de la primera condición en la segunda y queda:
x + x + y = y, reducimos términos semejantes, cancelamos términos y queda:
2x = 0, de donde despejamos: x = 0 (*);
luego reemplazamos el valor que hemos hallado en la primera condición y tenemos:
y = z (**).
Observa que hemos podido despejar dos incógnitas (x e y), por lo que planteamos:
x = 0
y = t
z = t
y un vector genérico del subconjunto queda expresado.
u = < 0 , t , t > = t< 0 , 1 , 1 >, con t ∈ R ,
con lo que tenemos que una base del subespacio es: B = { < 0 , 1 , 1 > }, y su dimensión es 1.
Luego, para demostrar con rigor que el subconjunto es un subespacio, tenemos:
1°) <0 , 0 , 0 > ∈ R³, tenemos qu: < 0, 0, 0 > = 0*< 0, 1 , 1 >, y el vector nulo pertenece al subconjunto.
2°) Tomamos dos vectores cualesquiera del subconjunto:
v = t1 * < 0 , 1 , 1 >, w = t2 * < 0 , 1 , 1 >, con t1 ∈ R y t2 ∈ R, y luego planteamos la suma:
v + w = t1 * < 0 , 1 , 1 > + t2 * < 0 , 1 , 1 > = (t1 + t2)*< 0 , 1 , 1 >, con t1 + t2 ∈ R (observa que tienes la suma de dos número reales),
y tenemos que la suma entre dos vectores del subconjunto pertenece al subconjunto.
3°) tomamos el múltiplo escalar genérico de un vector del subconjunto (k ∈ R):
k*v = k*( t1 * < 0 , 1 , 1 > ) = (k*t1)*< 0 , 1 , 1 >, con k*t1 ∈ R (observa que tienes el producto de dos números reales),
y tenemos que el múltiplo escalar genérico de un vector del subconjunto pertenece al subconjunto.
Luego, concluimos que el subconjunto es un subespacio vectorial de R³.
Espero haberte ayudado.
-
Muy buenas noches unicoos; cómo puedo demostrar que cada matriz cuadrada se descompone como suma de una matriz simétrica y de una matriz antisimétrica, y que, además, la descomposición es única. Gracias de antemano.
-
Como se hace este ejercicio?.
Utilizando argumentos de ortogonalidad entre subespacios halle un sistema de ecuaciones cuyo espacio de soluciones sea
S= = ⟨(−3, 0, 0, 4, 1), (0, 1, 2, 1, 0)⟩.
No entiendo lo de espacio de soluciones. Si yo tuviera un S ortogonal, las ecuaciones de S ortogonal serian las siguientes
S ortogonal: -3x +4w +u
y +2z + w
Pero no entiendo bien lo que pide el ejercicio.
-
Hola Unicoos, como están? necesito ayuda con este ejercicio, cuando me dice expresar el conjunto a través de la notación de modulo, la verdad es que no puedo expresarlo, agradecería su ayuda .



Antonio Silvio Palmitano
el 3/11/16Observa cuáles son las condiciones que deben cumplir los elementos del conjunto A:
x ≤ -3/2
x > -5, que leída de derecha a izquierda queda: -5 < x,
luego puedes escribir como una desigualdad doble:
-5 < x ≤ -3/2 (debemos tener en cuenta que esta desigualdad es amplia, y en el otro extremo es estricta):
Luego, promediamos los extremos y queda: (-5 -3/2)/2 = -13/4.
Luego restamos -13/4 en los tres miembros de la desigualdad doble y queda:
-5 + 13/4 < x + 13/4 ≤ -3/2 +13/4, resolvemos en los extremos y queda:
-7/4 < x + 13/4 ≤ 7/4, luego, como la doble desigualdad tiene extremos opuestos, podemos escribir:
|x + 13/4| < 7/4, observa que no hemos considerado la desigualdad amplia del miembro de la derecha, por lo que tenemos:
A = {x/x ∈ R y |x + 13/4| < 7/4} u { -3/2}.
Observa cuáles son las condiciones que deben cumplir los elementos del conjunto B:
-3 < x ≤ 0 (observa la desigualdad amplia a la derecha, y estricta a la izquierda),
|x| < 2, que puede expresarse: -2 < x < 2,
luego, los elementos que cumplen con ambas condiciones cumplen la condición:
-2 < x ≤ 0,
luego calculamos el promedio entre los valores extremos: (-2+0)/2 = -1, y restamos -1 en los tres miembros y queda
-2+1 < x+1 ≤ 0+1, luego resolvemos y queda:
-1 < x+1 ≤ 1, luego podemos escribir (observa que consideramos desigualdad estricta):
|x+1| < 1, luego escribimos:
B = {x/x ∈ R y |x+1| < 1} u {0}.
Espero haberte ayudado.