-
D.dani
el 3/11/16Hola pueden subir por favor un video de ecuaciones trigonométricas?
gracias
Ángel
el 3/11/16 -
The punk
el 3/11/16
Hola amigo me podrian ayudar con estas demostraciones no se como empezar como plantear la demostracion, es de partes de conjuntos
David
el 4/11/16
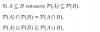
Antonio Silvio Palmitano
el 4/11/16Van esquemas de las demostraciones.
1) Sea X ∈ P(A) → por definición de conjunto de partes → X ⊆ A → (como A ⊆ B) → X ⊆ B → por definición de conjunto de partes → X ∈ P(B), por lo tanto; P(A) ⊆ P(B).
2) Sea X ∈ P(A) ∩ P(B) ↔ por definición de intersección ↔ X ∈ P(A) ∧ X ∈ P(A) ↔ por definición de conjunto de partes ↔ X ⊆ A ∧ X ⊆ B ↔ X ⊆ A ∩ B ↔ X ∈ P(A ∩ B ), por lo tanto:
P(A) ∩ P(B) = P(A ∩ B ).
3) Sea X ∈ P(A) ∪ P(B) → por definición de unión → X ∈ P(A) ∨ X ∈ P(B) → por definición de conjunto de partes → X ⊆ A ∨ X ⊆ B → X ⊆ A ∪ B → X ∈ P(A ∪ B), por lo tanto:
P(A) ∪ P(B) ⊆ P(A ∪ B).
Espero haberte ayudado.
-
Isabel
el 3/11/16 -
jorge jambo
el 3/11/16Para el cálculo de la monotonía de una función, ¿hay que tener en cuenta solo los máximos y mínimos o también los puntos que hagan 0 el denominador?
Y otra parecida:
Para el cálculo de la curvatura de una función, ¿hay que tener en cuenta solo los puntos de inflexión o también los puntos que hagan 0 el denominador?
-
raul garcia
el 3/11/16Tengo bien mis deberes
a es divisible entre b si y he puesto esto me venia un hueco he puesto a : veni un hueco he puesto b es venia un hueco he puesto a
Ángel
el 3/11/16 -
Laura
el 3/11/16Buenas, tengo una pregunta sobre un ejercicio de matrices. El ejercicio me pide A^128, siendo la matriz (4 5 -1)
A= (-3 -4 1)
(-3 -4 0)
He realizado A2 y A3 y no tienen nada que ver el resultado de unas con otras. Entonces no encuentro la forma de hallar A^128.
Gaizka
el 3/11/16Hola Laura!
Este es un caso especial, ya que A^3 es igual a I3 (matriz identidad). Esto quiere decir que A es una matriz periódica de periodo p=3.
En las matrices periódicas se cumple que A^(p+1) = A.
En otras palabras, el producto de A e I3 es igual a A. Por lo que:
A^4 = I3 * A = A
A^5 = A^4 * A = A * A = A^2
A^6 = A^5 * A = A^2 * A = A^3 = I3
A^7 = A^6 * A = I3 * A = A
etc.
Sabiendo que el periodo es 3, es muy sencillo calcular A^n. Solo hay que dividir n/3:
- Si n es múltiplo de 3, entonces A^n = I3
- Si n no es múltiplo de 3 entonces la división n/3 queda con resto. A^n será igual a A elevado a ese resto ("multiplicado por I3 elevado al resultado de la división n/3"esto es como multiplicar por 1 :D)
Te dejo el ejercicio resuelto.
-
Facundo Meier
el 3/11/16Tengo otra duda con el siguente ejercicio, Lim x→inf (2^x)/(e^x), tengo que calcularlo por L´Hopital
Lo que hice fue aplicar la regla, primero derivando, entónces lim de x→inf de 2^x. ln (2)/ (e^x),
Pero sigue quedando indeterminado inf/inf, me pueden ayudar por favor.
Gracias
-
Augusto
el 3/11/16Por que lim(1+1/n)^n=e y no 1 cuando tiende a infinito si 1/n es 0 y 1^n es 1?
Ángel
el 3/11/16Porque 1/infinito= 0+ : nunca llega a ser exactamente cero
Entonces 1 + 0+= 1+
(1+) infinito = ..................
(un tal Matthew Hebert llevaba el año pasado más de 1,4 billones de cifras calculadas, pero como puedes comprobar, el lim(1+1/n)^n nunca será menor de 2,718...por muy grande que sea el número "n" )
-
Pablo
el 3/11/16Como formar un complejo a partir de esto?.
Tengo el siguiente complejo: z^2 + 2z - 2iz - 18i = 0
Creo que tengo que hacer a partir de cuadrado de un binomio formar el complejo.
He intentado a ojo hacer cuadrado de un binomio para llegar a la forma de arriba, intente hacer (z-i)^2 y me queda z^2 -2iz -1 pero no encuentro la forma de que me quede algo parecido a lo de arriba.
Antonio Silvio Palmitano
el 3/11/16Tienes la ecuación:z^2 + 2z - 2iz - 18i = 0,agrupas términos lineales y queda:z^2 + 2(1-i)z - 18i = 0,haces pasaje de término, completas binomio elevado al cuadrado a la izquierda:z^2 + 2(1-i)z + (1-i)^2 = 18i + (1-i)^2,factorizas a la izquierda, desarrollas y reduces términos semejantes a la derecha:(z + 1-i)^2 = 16i,expresas en forma polar a la derecha (tienes módulo 16 y argumento pi/2):(z + 1-i)^2 = (16)(pi/2),haces pasaje de potencia como raíz:z + 1-i = V( (16)(pi/2) ),aplicas la fórmula de De Moivre para las raíces:z + 1-i = ( V(16) )( (pi/2 + 2kpi)/2 ), con k=0,1,luego tenemos dos opciones para el segundo miembro de la ecuación:a) (4)(pi/4) = expresamos en forma trigonométrica:= 4(cospi/4 + isenpi/4) = distribuimos:= 4cospi/4 + i4senpi/4;luego la ecuación queda:z + 1-i = 4cospi/4 + i4senpi/4,hacemos pasajes de términos, agrupamos términos reales e imaginarios y queda:z = (-1 + 4cospi/4) + i(1 + 4senpi/4) (*), aproximamos valores:z = 1,82 + 3,82i.b) (4)(5pi/4) = expresamos en forma trigonométrica:= 4(cos5pi/4 + isen5pi/4) = distribuimos:= 4cos5pi/4 + i4sen5pi/4;luego la ecuación queda:z + 1-i = 4cos5pi/4 + i4sen5pi/4,hacemos pasajes de términos, agrupamos términos reales e imaginarios y queda:z = (-1 + 4cos5pi/4) + i(1 + 4sen5pi/4) (**), aproximamos valores:z = -3,82 - 1,82i.Por lo tanto, concluimos que las soluciones de la ecuación sonz1 = (-1 + 4cospi/4) + i(1 + 4senpi/4) (*).z2 = (-1 + 4cos5pi/4) + i(1 + 4sen5pi/4) (**).Espero haberte ayudado.Responde esta pregunta... -
Pablo
el 3/11/16Como se grafica este tipo de complejos. Tengo una duda con graficos de numeros complejos.
El ejercicio es asi: |3z+3-6i|≤9
Generalmente en los ejercicios de mi practica nos daban que el complejo era mayor a un angulo y menor a otro y nos daban el argumento.
En este caso me dan que el modulo es menor o igual a 9. El problema es que no se que hacer con el 3Z. Porque lo que se me ocurre si no estuviera el 3 multiplicando es hacer
|z-(-3+6i)|<=9 ...Entonces desplazaria el complejo 3 en x y 6 para arriba y haria un circulo dentro del cual estaria el complejo (No se si esto estaria bien), el tema es que no se que hacer con el 3 multiplicando al Z. Muchas gracias
