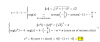-
Víctor Miranda
el 29/10/16Alguien me puede ayudar con el ejercicio 10?
Antonio Silvio Palmitano
el 29/10/16Tienes, a partir del enunciado, los siguientes datos:
Escuchan A y B: 10%
Escuchan sólo A: 25% (observa que el 35% escucha la emisora A)
Escucha sólo B: 18% (observa que el 28% escucha la emisora B)
No escucha ni A ni B: 47%
Total: 100%.
Es muy conveniente que hagas un diagrama de Venn, para visualizar mejor la situación.
Luego pasamos a responder:
a) p(AuB) = P(A) + p(B) - p(A∩B) = (35 + 28 - 10)/100 = 53/100 = 53%.
b) p(AUB) ' = 1 - p(AuB) = 1 - 53/100 = 47/100 = 47% (indicamos complemento con ' ).
c) p(A|B ' ) = p(A∩B ')/p(B ' ) = p(A∩B ' )/( 1 - p(B) ) = (25/100) / ( 1 - 28/100 ) = (25/100) / (72/100) = 25/72 = 34,72%.
d) p(A|B) = p(A∩B)/p(B) = (10/100) / (28/100) = 10/28 = 35,71%.
e) p( (A-B)u(B-A) ) = p( (AuB)-(A∩B) ) = p(AuB) - p(A∩B) = 53/100 - 10/100 = 43/100 = 43%.
Debes tener en cuenta las probabilidades de:
unión de sucesos, intersección de sucesos, suceso complementario, diferencia de sucesos;
y la probabilidad condicional de un suceso dado que ocurre otro.
Espero haberte ayudado.
-
celia curin
el 29/10/16estoy horas con este ejercicio de maximos y minimos 2x/x²+1 ... no me sale el resultado de la segunda derivada..
resultado de max y min: f ′′(1) = 4 < 0 ⇒ f ( x)tiene un máximo relativo en xc =−1 y f"(-1)= 4 > 0 ⇒ f ( x) tiene un mínimo
relativo en xc = −1
Antonio Silvio Palmitano
el 29/10/16Observa que el dominio de la función es: D = (-inf,+inf) = R.
Has planteado bien la expresión de la derivada primera y la condición de punto crítico (o singular), y has obtenido los dos puntos críticos (x1 = -1, x2 = 1) correctamente.
Luego pasamos a la derivada segunda:
Observa que la expresión de la derivada primera es un cociente u/v, con:
u = -2x^2 + 2, de donde tienes: u ' = -4x
v = (x^2 + 1)^2, de donde tienes: v ' = 2(x^2 + 1)*2x = 4x(x^2 + 1),
luego, la expresión de la derivada segunda queda: f ' ' (x) = ( u ' * v - u * v' ) / v^2, veamos su numerador (N) y su denominador (D) por separado:
N = u ' * v - u * v ' = -4x*(x^2 + 1)^2 - (-2x^2 + 2)*4x(x^2 + 1) = extraemos factor común = 4x(x^2 + 1)*( -(x^2 + 1) - (-2x^2 + 2) ) = 4x(x^2 + 1)(x^2 - 3)
D = v^2 = ( (x^2 + 1)^2 )^2 = (x^2 + 1)^4
Luego, la expresión de la derivada segunda queda:
f ' ' (x) = N/D = simplificamos = 4x(x^2 - 3) / (x^2 + 1)^3 (observa que exista para todo número real).
Luego, pasamos al análisis de los puntos críticos, y para ello los evaluamos en la expresión de la derivada segunda:
f ' ' (-1) = 4(-1)( (-1)^2 - 3 ) / ( (-1)^2 + 1 )^3 = -4(-2)/2^3 = 8/8 = 1 > 0, por lo que tenemos concavidad hacia arriba, y concluimos que la función presenta un mínimo en x1 = -1.
f ' ' (1) = 4(1)( (1)^2 - 3 ) / ( (1)^2 + 1 )^3 = 4(-2)/2^3 = -8/8 = -1 < 0, por lo que tenemos concavidad hacia abajo, y concluimos que la función presenta máximo en x2 = 1.
Espero haberte ayudado.
-
Usuario eliminado
el 29/10/16Hola, me podrian ayudar a encontrar el dominio de esta funcion?
Antonio Silvio Palmitano
el 29/10/16Por favor, verifica que hayas copiado bien la expresión de la función.
Porque si observas bien el denominador, tienes para su segundo factor (que es una raíz cuadrada): -x>0, que al despejar queda: x<0;
y para el primer término del segundo factor (que es un logaritmo): x - 1>0, que al despejar queda: x>1;
y observa que las dos condiciones son excluyentes (no existe un número real x que sea menor que cero y mayor que uno a la vez), por lo que tenemos que el dominio de la función es el conjunto vacío.
-
Albano Caminos
el 29/10/16Buenas, quisiera saber si me pueden dar una mano con el siguiente te ejercicio!
-
Alex Domínguez
el 28/10/16ME ayudan con este ejercicio de diagonalizar ? No se ni por donde cogerlo
7. En cada uno de los siguientes casos, diagonalice, si es posible, el endomorfismo f : R 3 → R 3 proporcionando una base Baut de R 3 formada por autovectores, la matriz P de cambio de base de Baut a la base canónica Bc y la matriz D asociada a f respecto de la base Baut.
c) f(x, y, z) = (5x − 4z, 3y, 2x − z)
-
Alex Domínguez
el 28/10/16Como puedo resolver el polinomio con incógnitas tal que así
λ2 -2λ -pλ -2p = 0
Gracias
Ángel
el 28/10/16
Antonio Silvio Palmitano
el 28/10/16Si la incógnita a despejar es lambda (indicamos con L, y la indeterminada p es real), observa que la ecuación puede escribirse:
L^2 - (2+p)L - 2p = 0, que es una ecuación polinómica cuadrática, cuyos coeficientes son:
A = 1, B = -(2+p), C = -2p.
Luego observa que el discriminante de la fórmula resolvente queda:
D = B^2 -4AC = (-(2+p))^2 - 4*1*(-2p) = 4 + 4p + p^2 + 8p = p^2 + 12p + 4.
Y por último, observa que las soluciones quedan
L1 = (2 + p +V(D))/2
L2 = (2 + p - V(D))/2
Observa que pueden presentarse tres casos:
Si D > 0, tenemos dos soluciones reales distintas
Si D = 0, tenemos una solución real doble
Si D < 0, tenemos dos soluciones complejas.
Espero haberte ayudado.
-
Arz
el 28/10/16
-
Raisa
el 28/10/16Antonio serias tan amable de ayudarme? Gracias besitos :)
Ejercicio 5
A 120 alumnos de Bachillerato se les subvenciona una excursión con destino a las comunidades de Andalucía, Galicia y País Vasco, con un total de 8 922 €. Se asignan 60 € a cada alumno con destino a Andalucía, 72 € a cada uno que vaya al País Vasco y 90 € a los que se
dirigen a Galicia. Además, el total de alumnos que van a las dos primeras comunidades citadas excede en 50 a los que van a Galicia. Halla el número de alumnos que visita cada comunidad
-
Laura
el 28/10/16Hola, necesito ayuda con este ejercicio, tengo que hacer rotar alrededor del eje Y esa funcion pero no me da el resultado del libro, no se si tampoco lo grafique bien. Despeje la X y la eleve al cuadrado y luego calcule la integral. Creo que no se ve bien a que esta elevado la funcion, asi que aclaro: el x,a,y estan elevados a la 2/3
Antonio Silvio Palmitano
el 28/10/16Observa que los puntos de intersección de la curva con los ejes coordenados son:
(0,-a) y (0,a) con el eje OY,
(-a,0) y (a,0) con el eje OX.
Observa también que la curva es simétrica con respecto a los dos ejes coordenados, y que has dibujado el sólido correspondiente a su mitad superior.
Y observa que los límites de integración deben ser 0 y a (has consignado 0 y 1 en tu trabajo), y que has integrado la mitad superior de sólido.
Luego, observa que si corriges el límite superior de integración, y resuelves entre 0 y a, el volumen de la mitad superior queda:
V = pi * a^3 ( 1 - 9/5 + 9/7 - 1/3 ) = (16/105)pi * a^3.
Luego, por simetría el volumen total queda:
Vt = 2*(16/105)pi * a^3 = (32/105)pi * a^3.
Espero haberte ayudado.
-
Matias Encinas
el 28/10/16Me podrían ayudar con este ejercicio, no se como utilizar al fórmula de Moivre si alguien sería tan amable de ayudarme.
Expresa (1-i) en forma trigonométrica y utiliza la fórmula de Moivre para obtener el valor de la potencia: (1-i)4
